回覆:我在想:我也要试试手机上阿斯兰侃吧阿斯兰侃吧还没开发手机版
|
自由灌水 |
回覆:啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊 |
回覆:【百度百科】超正方体超正方体的顶点坐标可以用类比的方式推导:
正方形的坐标:(±1,±1) 正方体的坐标:(±1,±1,±1) 那么类比可以得到四维超正方体的顶点:(±1,±1,±1,±1)... |
回覆:【百度百科】超正方体超正方体Tesseract的施莱夫利符号有几个
{4,3,3}(特指它是正多胞体Tesseract); {4,3}x{}(代指Cubic prism); {4}x{4}(4-... |
回覆:【百度百科】超正方体零维的一个点,包含一个零维元素(点);一维的一条线段,包含一个一维元素(线段),两个零维元素;二维的一个正方形,包含一个二维元素(面),四个一维元素;三维的一个正方体,包含 一个三维元素(三维...
|
回覆:【百度百科】超正方体 [圖片]大家一定知道把立方体的六个面展开的样子吧,其中一种展开法如右图。
类比一下,即可得到超正方体的其中一种展开法,如最右图,其中一个立方体被藏在三维展开图里边了。... 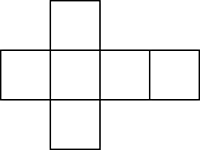  |
回覆:【百度百科】超正方体 [圖片]思维方式
如果四维超正方体不太好想象的话,我们换成球试试吧。三维球嘛,无论从哪个方向投影在二维平面上都只是一个半经等同的圆形,这样我们就很容易想到四维球在三维世界中的投影只不过是一个...   |
回覆:【百度百科】超正方体 [圖片]施莱格尔投影
四维方体不易想象,但可以投射至3维或2维空间。在2维平面的投射,把顶点位置调整后,可以了解更多。如此获得的图像,不再反映四维方体空间构造,而是反映顶点间的联系。... 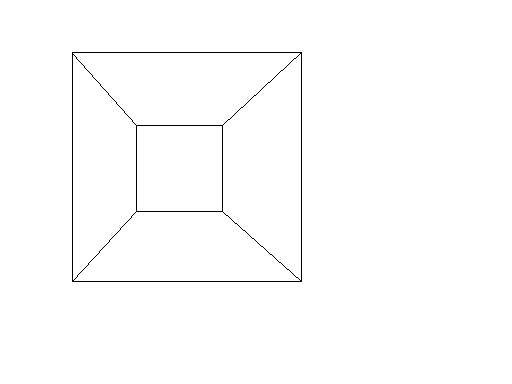 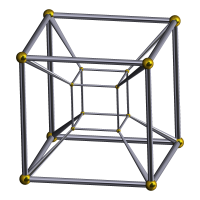 |
回覆:【百度百科】超正方体超立方体,又作正八胞体(8-cell,Regular octachoron),立方体柱(Cubic prism),4-4边形柱(4-4 duoprism),是一个四维空间里的几何产物
需... |