所有帖子_Purasbar

全站共有主题数31796个，帖子数147290篇。

点击	回复	标题	作者	最后回复
630	0	吃了豌豆胡豆打屁pang臭	4Der	4-23 4Der
743	0	吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭	4Der	4-23 4Der
733	0	吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭	4Der	4-23 4Der
704	0	吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁pang臭吃了豌豆胡豆打屁p...	4Der	4-23 4Der
716	0	吃了豌豆胡豆打屁pang臭	4Der	4-23 4Der
668	0	複製本帖地址回複數：70 點擊數：102 本吧熱門帖子侃吧最高樓韓國鈞咖啡館侃吧公告複製本帖地址回複數：70 點擊數：102 本吧熱門帖子侃吧...	4Der	4-23 4Der
605	0	恭喜本吧出現了「本吧熱門貼子」魔塊 rt	4Der	4-23 4Der
537	0	速度東安雞歐莎大家 0大事件jf0ujsadj0jf0osdj	魔法绿骑士	4-23 魔法绿骑士
645	0	多維黃瓜	4Der	4-23 4Der
968	2	根號-i-1是多少 -i-1=(-1,-1) 設根號(-1,-1)=(x,y) 則 x²-y²=-1 2xy=-1	4Der	4-23 yaoliding
970	9	【轉載】不同維度的對話：帶你進入四維世界上次說到維度時，有人提到了如何理解四維空間的問題。這是一個非常有趣的話題，可是我一直沒有用心寫一下。前段時間網上出了一部片子叫做Dimensions: a walk through mathemati...	4Der	4-23 118.117.5.*
1097	0	維基百科藥家鑫 http://zh.wikipedia.org/w/index.php?title=%E8%8D%AF%E5%AE%B6%E9%91%AB&variant=zh-cn	Revive_ctg	4-23 Revive_ctg
895	0	您好，阿斯蘭侃吧歡迎您的到來~ 親愛的用戶：歡迎來到藥家鑫吧，阿斯蘭侃吧歡迎您的到來~ 請先閱讀我們的社區準則：http://documents.arslanbar.net/eula/zh/ 以及版權聲明：htt...	社区管理员	4-23 社区管理员
899	4	與廣告費	Revive_ctg	4-23 Revive_ctg
889	1	風格和健康	Revive_ctg	4-23 Revive_ctg
764	1	與u一家	Revive_ctg	4-23 Revive_ctg
883	2	體罰	Revive_ctg	4-23 Revive_ctg
868	1	傢伙	Revive_ctg	4-23 Revive_ctg
748	1	個	Revive_ctg	4-23 Revive_ctg
716	1	呵呵	Revive_ctg	4-23 Revive_ctg
832	1	哈飛股份	Revive_ctg	4-23 Revive_ctg
895	1	個	Revive_ctg	4-23 Revive_ctg
892	5	和可信度和海地可是哈哈哈大賽開始	Revive_ctg	4-23 Revive_ctg
741	4	會不會	Revive_ctg	4-23 Revive_ctg
760	1	的時候	Revive_ctg	4-23 Revive_ctg
648	1	四大發發是打發	Revive_ctg	4-23 Revive_ctg
755	6	四大發發打死	Revive_ctg	4-23 Revive_ctg
984	5	關於24-cell線段的問題線：2×（12+4+6×4）+（8+1+6）=95 和影片不符啊，我少算了哪條線？	4Der	4-22 yaoliding
915	0	影片的第二集，一隻蜥蜴從紙上爬出來，然後冒出一個正12面體 rt	4Der	4-22 4Der
876	4	把三維球體球極投影到二維平面，那麼會佔滿整個二維空間若把四維球體球極投影到三維空間，就會佔滿整個三維空間（。。。）！	4Der	4-22 4Der
1119	5	系統多面體：透視模型這個不是已經上傳了麼 rt	4Der	4-22 yaoliding
768	0	多胞體各種維度的面的名稱及簡稱維度全稱簡稱 0 零維面點 1 一維面線或棱 2 二維面面 3...	4Der	4-22 4Der
798	0	我認為影片中第三集的魔術黑板其實是三維平面普通黑板也就是四維空間中的普通黑板，其表面是三維，所以能畫三維圖形	4Der	4-22 4Der
1035	4	有沒有三維星形多面體的圖片和動畫？我要類比學習四維星形多胞體	4Der	4-22 yaoliding
1028	9	我發現平行投影嚴重破壞了120胞體的形態，但球極投影就不一樣了平行投影嚴重破壞了120胞體的形態，導致各個正12面體互相相交，分不清誰是誰。但球極投影後，各個12面體就挨個挨個的擺在一起，沒有重合，很容易分辨。當然超正方體也是一樣的，直接看平行投...	4Der	4-22 yaoliding
1078	2	汗，其實我想問一下，沒必要一兩句話就發個帖吧一個貼的內容太簡單了，我覺得不如集中到一個貼里有想說的話的時候留個言我希望這吧可以像四維空間吧那麼多一點人去討論一下	yaoliding	4-22 yaoliding
1186	6	【文章】關於拼四維球體在二維空間中，我們給蜥蜴幾個三維球體的橫截面——即各種大小不同的圓，讓蜥蜴在二維空間去拼三維球體，結果二維空間的蜥蜴根本拼不出來，他只是把各個圓擺在了一起，沒有拼成真正的球體。我們也一樣，給我...	4Der	4-22 yaoliding
896	2	我認為在三維空間中任意選取五個點並兩兩相連畫正五胞體更好些就好比四維生物在三維平面上畫正五胞體	4Der	4-22 yaoliding
831	2	三維超球面上是經面，緯面，而不是「線」 rt	4Der	4-22 yaoliding
944	1	一道四維單形的證明題 [图片] 任意五胞體EABCD自五個頂點分別引出四條直線（每個頂點不同顏色）使得自這一頂點引出的四條直線所組成的五胞體的各側四面體所成二胞角分別為以這一點為頂點對應的原五胞體EABCD各側四面體所成二胞角的3...	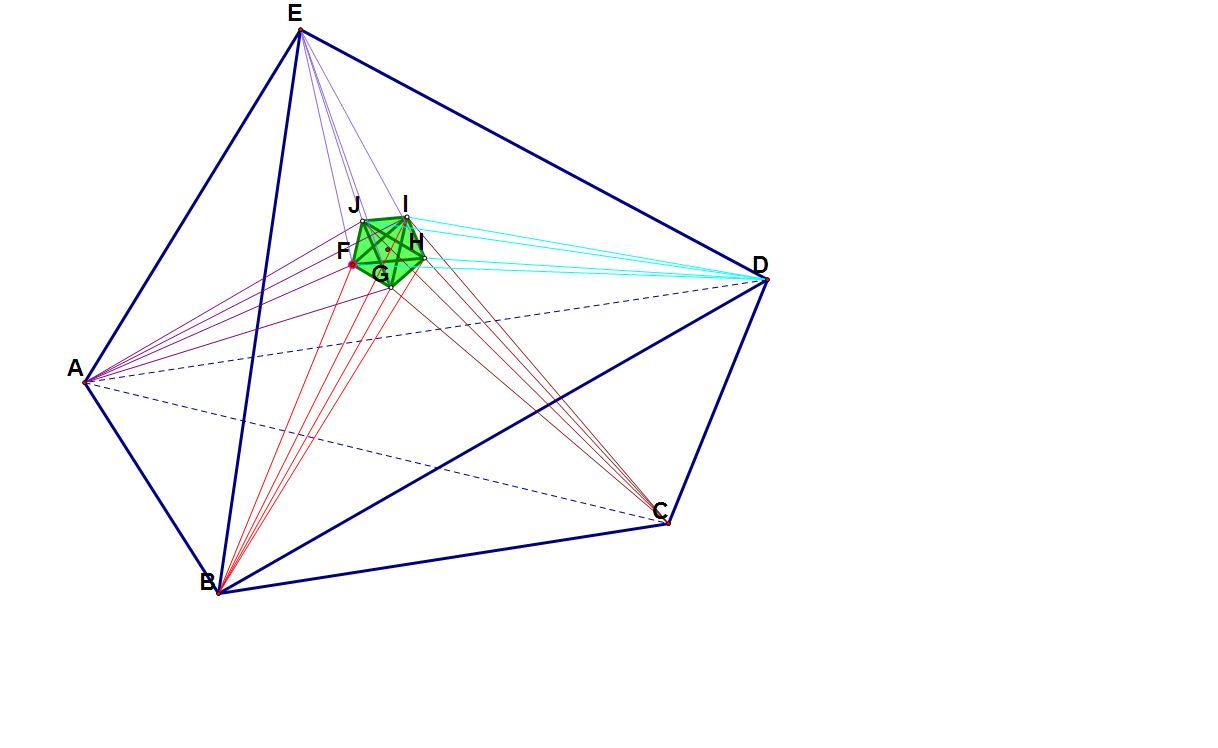4Der	4-22 yaoliding
1015	1	這個圖不會就是四維輪胎吧？ [图片]	4Der	4-22 yaoliding
1059	2	請吧主進來幫我解決個問題正多胞體定義：它是一個四維空間上的多胞形(Polytope,點、線段、多邊形、多面體，以及更高維度的幾何物體的總稱) 多胞體表面(Facet)由有限個正多面體組成，每個頂點情況相...	695223183	4-22 yaoliding
909	1	通過五維單形的球極投影，可以數出有6個頂點 [图片]	4Der	4-22 yaoliding
990	2	【個人認為】4D文字和超正方體的推倒差不多就是把3D文字複製一份，然後連接各個頂點	4Der	4-22 yaoliding
1140	4	【調查一下】各位都是幾年級的 [投票]	4Der	4-22 yaoliding
929	5	關於三維球面的橫截面二維的圓，可以由無數個從短到長，再到短的直線拼成三維的球，可以有從小到大，再到小的二維圓拼成那麼，四維的球就是從小到大，再到小的三維球體拼成了	4Der	4-22 yaoliding
810	1	各種正多胞體的三維類比 5-cell：四面體 8-cell：正方體 16-cell：八面體 24-cell：無 120-cell：十二面體 600-cell：二十面體	4Der	4-22 yaoliding
903	1	【flash】1-4維的正方體	4Der	4-21 4Der
661	1	2011年4月21日	64.34.204.*	4-21 64.34.204.*
892	5	超正方體的體積計算公式 V4=a^4	218.88.141.*	4-19 4Der
首页上一页 518 519 520 521 522 523 524 525 526 527 下一页尾页

	©2010-2025 Purasbar Ver3.0 ▲
	除非另有声明，本站采用知识共享署名-相同方式共享 3.0 Unported许可协议进行许可。

一道四維單形的證明題 [图片]

這個圖不會就是四維輪胎吧？ [图片]

通過五維單形的球極投影，可以數出有6個頂點 [图片]

【調查一下】各位都是幾年級的 [投票]