【flash】1-4维的正方体 |
超正方体的体积计算公式V4=a^4
218.88.141.*
4-19
4Der
(點擊/回復: 822/5)
|
貌似施莱格尔投影和球极投影都不是物体的原型用手电筒照一个四维物体叫什么投影?
4Der
4-18
219.137.36.*
(點擊/回復: 715/1)
|
这些是不是多胞体的展开图 [圖片]24cell:
 |
话说我认为多维图形的二维线架图很像分形的说并且维数越高分形图形越精细
|
【问题】五维单形大概有多少个四维单形?rt
|
【图片】正多胞体的三维展开图http://zh.arslanbar.net/pictures.php?b=%E5%9B%9B%E7%BB%B4%E5%87%A0%E4%BD%95%E5%AD%A6&label=album...
|
前十维基本多胞形表格,看的懂的求陪同 [圖片]我写的
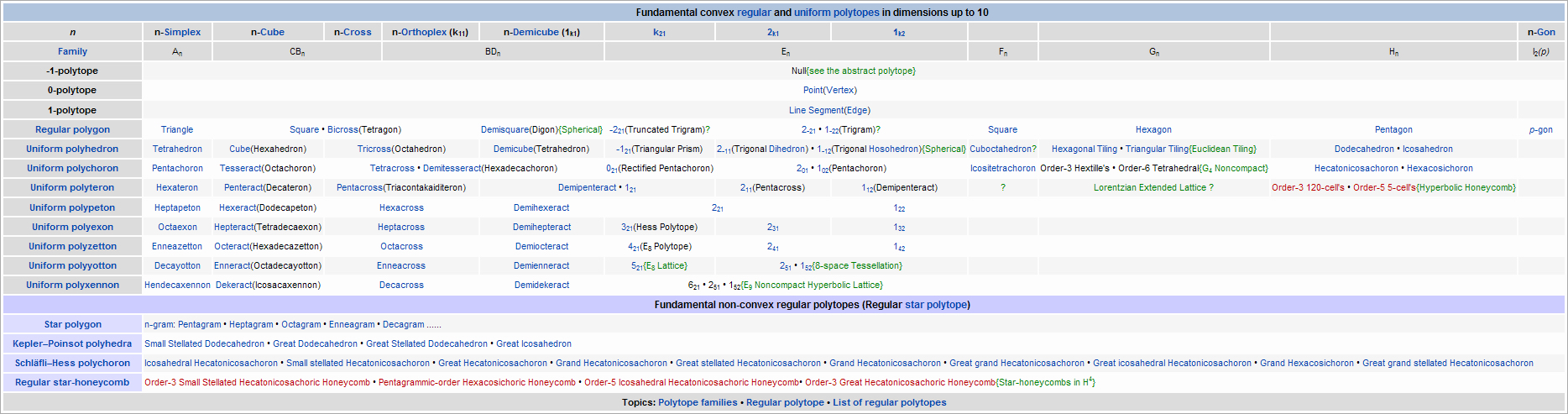 |
各种三维正多面体的球极投影都是jenn里面的rt
|
其实各种多胞体表面都是三维不仅仅是超球
|
在阿斯兰侃吧中发帖过快不会被系统自动封禁http://zh.arslanbar.net/post.php?i=12737
你看,某人灌了那么多,都没被封过 但如果是百度那就不一样了,灌到200多层就会删帖+系统自动永久封禁... |
三维空间很容易想像但三维平面就很难想像了,因为涉及到四维空间
|
【公告】我启用了在主题列表显示精品贴所属分类的功能【资料】正多胞体 [高维基础] [置顶]
意思是说这个帖子是精品贴,所属分类为“高维基础”。此时“高维基础”这四个字是淡蓝色 |
现在百度贴吧一个贴子删除后,是只能恢复五楼,还是能全部恢复?rt
|
把四维超球球极投影后会填满整个三维空间???那些正多胞体也是扩充成球后进行球极投影的,为何不填满整个三维空间?
|
| 本吧共有主題數196個,帖子數831篇,四維愛好者數7位。 |
內容轉換: |