【一道題】正方形坐標題 [圖片]如圖,已知四邊形ABCO是正方形,O是原點。點E為AB的中點。連接AC、BO,交於點F,且C點的坐標為(7,1)。
(1)...  |
我在jenn中弄出了12面體 [圖片]
魔法绿骑士
5-2
125.67.191.*
(點擊/回復: 997/7)
|
【動畫】在四維空間中旋轉三維正方體 [圖片] |
【圖片】在三維空間中畫正五胞體 [圖片]先看看在二維的紙上畫三維的正四面體。先畫四個點,然後每個點兩兩相連,共畫六條棱。
畫出來後發現有兩條棱相交了,但實際上根本沒有相交。並且,後面的那條橫著的棱被兩個面擋住了,所以畫成虛線。... 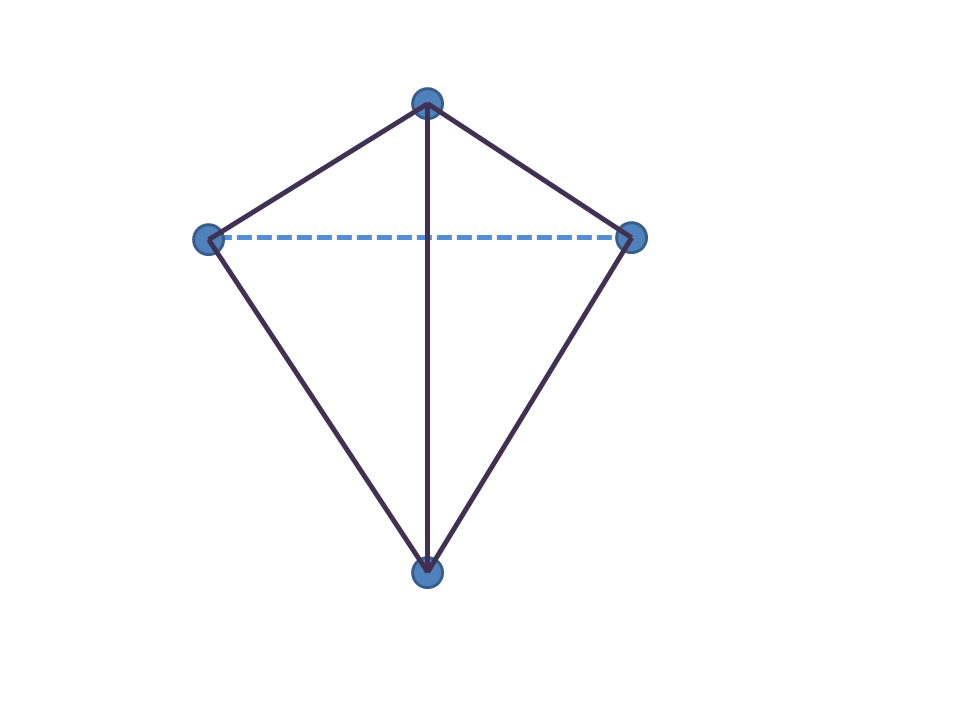 |
【轉載】【科普向】教你觀察和想像四維空間 [圖片]愛因斯坦說:四維?有啊,時間就是第四維
扯他的蛋去吧。我這裡將要說的四維空間,是指純幾何意義上的思維。 在兩百年以前,人們普遍認為數學是一種工具,是要為現實服務的。...  |
【圖片】三維多面體的施萊格爾投影 [圖片] |
【圖片】正多胞體的旋轉圖 [圖片]600-cell
 |
一道四維單形的證明題 [圖片]任意五胞體EABCD自五個頂點分別引出四條直線(每個頂點不同顏色)使得自這一頂點引出的四條直線所組成的五胞體的各側四面體所成二胞角分別為以
這一點為頂點對應的原五胞體EABCD各側四面體所成二胞角的3...
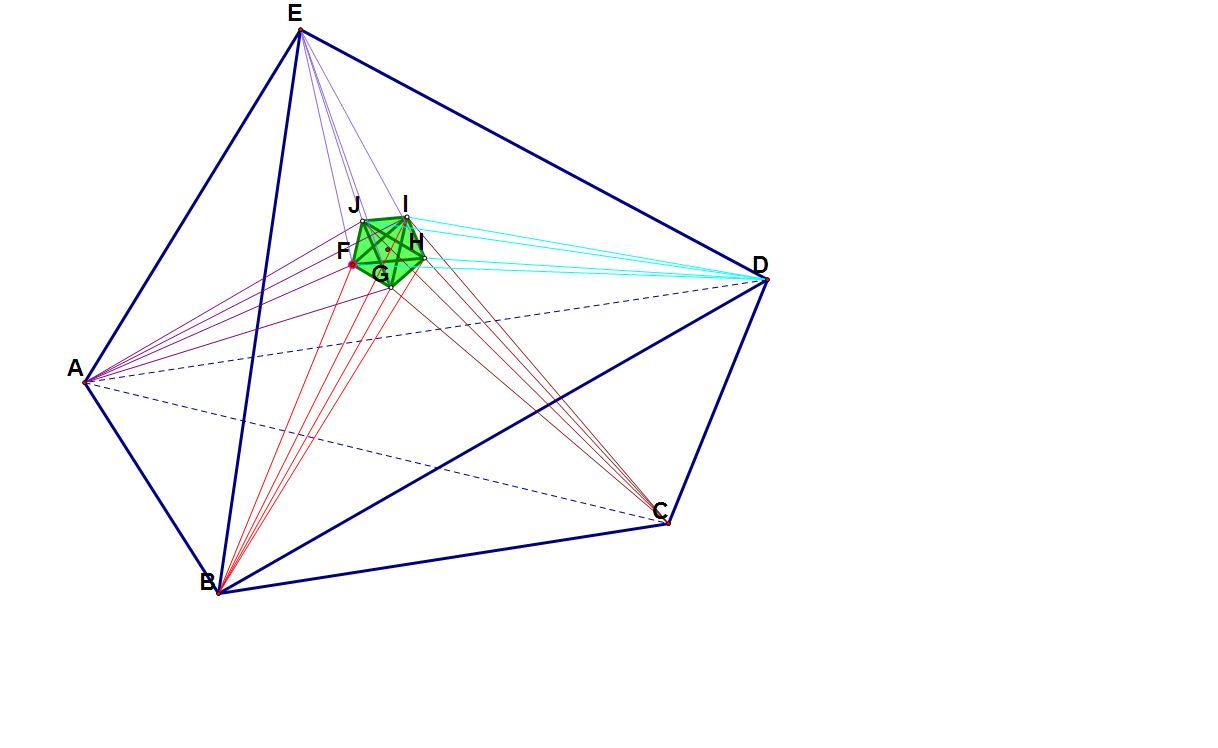 |
這個圖不會就是四維輪胎吧? [圖片] |
通過五維單形的球極投影,可以數出有6個頂點 [圖片] |
這些是不是多胞體的展開圖 [圖片]24cell:
 |
前十維基本多胞形表格,看的懂的求陪同 [圖片]我寫的
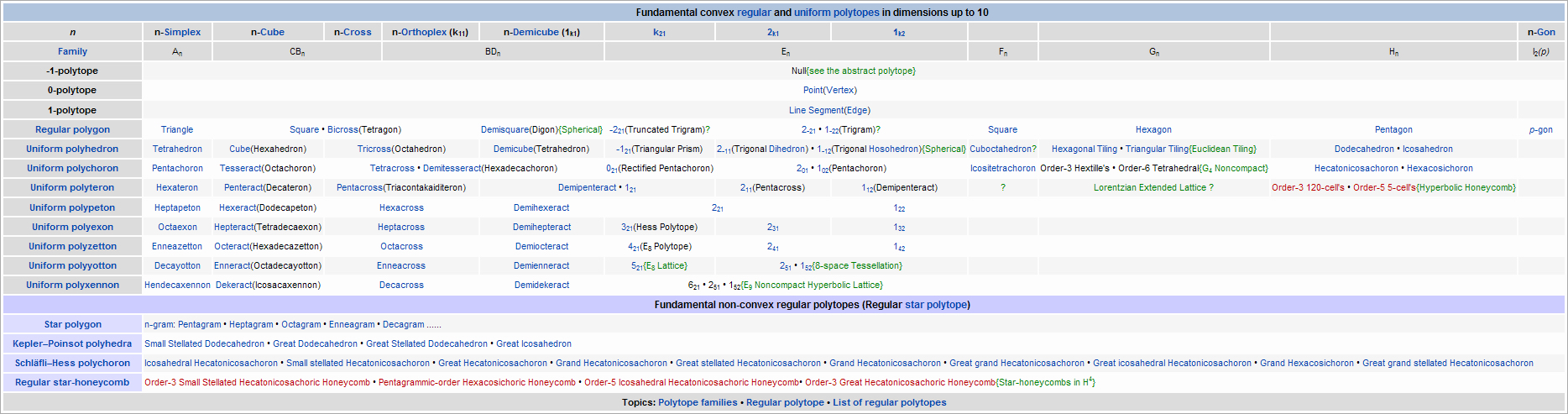 |
jenn中滾動球極投影 [圖片]這是影片中的8-cell第二種類型的球極投影滾動動畫中的一幕:
時間大約是5:39  |
【轉載】Fundamental convex & non-convex uniform po [高維基礎] [圖片]寫這個估計沒人懂的了,我自娛自樂好了
順便BS一下百度相冊,最長邊最多隻有1600像素,乾脆用網易好了 再BS一下,bmp圖居然不能點擊看大圖 一個我在英文wiki上自己改的Poly...  |
【圖片】jenn3d也可以進行球極投影滾動 [圖片] |
| 本吧共有33篇圖片帖。 |
內容轉換: |