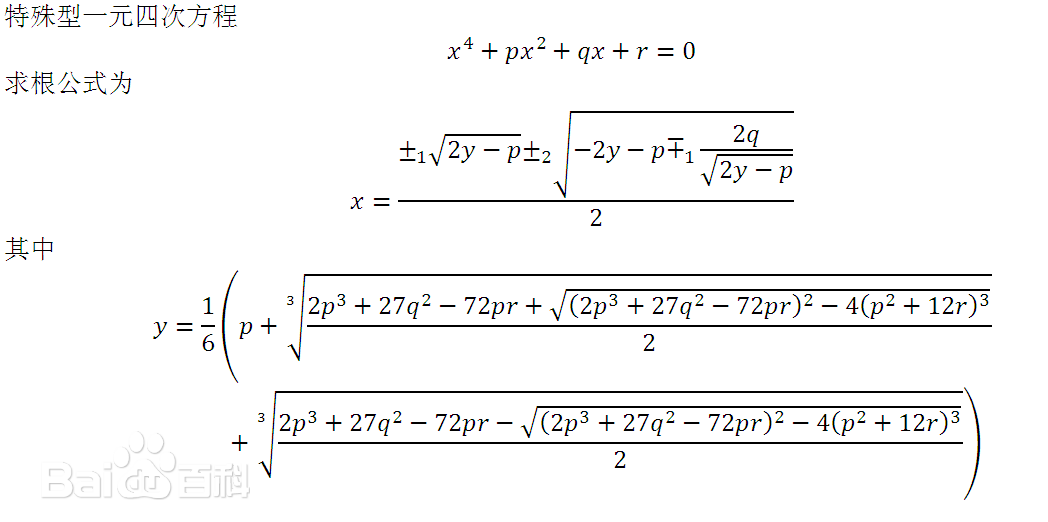https://zh.purasbar.com/post.php?t=26279
原文不严谨,所以删了修改后重发。
对于特殊型一元四次方程x4+px2+qx+r=0,如果q=0,那么这个方程就是AB类方程(简单四次方程)。
AB类方程之所以又叫简单四次方程,是因为这类方程形式上非常简单,主要包括
(1)只含四次项和常数项的方程:ax4+e=0
因为b=c=d=0,q的分子为0,所以q=0,方程属于AB类
(2)双二次方程:ax4+cx2+e=0
因为b=d=0,q的分子为0,所以q=0,方程属于AB类
(3)能直接用配方法求解的四次方程,如x4+4x3+6x2+4x-5=0,可以配成(x+1)4-6=0
方程能用配四次方法直接求解,说明x=y-b/4a换元后得到的方程y4+py2+qy+r=0不含三、二、一次项。因此p=q=0。因q=0,所以方程属于AB类