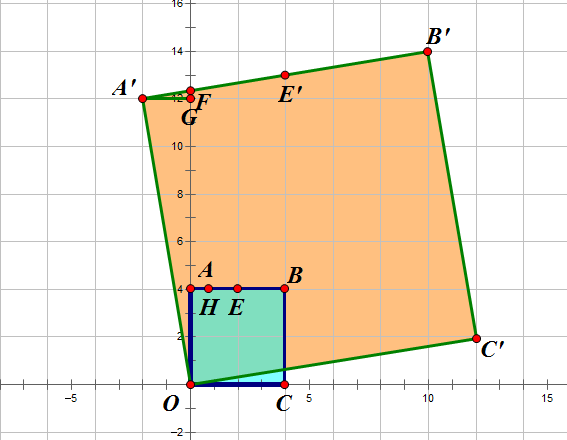如圖，已知四邊形ABCO和四邊形A』B』C』O都是正方形，且B的坐標為(4,4)，AB=4，C』的坐標為(12,2)，求：
(1)     A』和B』的坐標；
(2)     若E』是A』B』的中點，求E』的坐標；
(3)     若A』B』交y軸於F，求△A』FD的面積；
(4)     若H是AB上一點，且A』F:A』B』=AH:AB，求H的坐標。

解：(1) C=B-ABi=(4,4)-(0,4)=4
k=C』÷C=(12,2)÷4=(3,0.5)
B』=Bk=(4,4)×(3,0.5)=(12-2,12+2)=(10,14)
A=B-AB=(4,4)-4=(0,4)
A』=Ak=(0,4)(3,0.5)=(0-2,12+1)=(-2,12)

(2) 作AB的中點E，AE=AB÷2=4÷2=2
∵A=(0,4)，∴E=A+AE=(0,4)+2=(2,4)
E』=Ek=(2,4)×(3,0.5)=(2×3-4×0.5,4×3+2×0.5)=(6-2,12+1)=(4,13)
 
(3)設A』B』的解析式為y=kx+b
則b-2k=12，10k+b=14
解得k=1/6  b=37/3
∴y=(x+74)/6
當x=0時
y=74/6=37/3
∴DF=37/3
作A』G⊥FD於G，則AG=2
∴S△A』FD=37/3*2/2=37/3
 
(4)           F=(0,37/3)
H=F/k=(0,37/3)÷(3,0.5)=(0+37/6,37-0)÷(9+0.25)
=(37/6,37)÷(37/4)
=[(37/6)×(4/37),37×(4/37)]
=(2/3,4)

話說這道題貌似連勾股定理都不能解。只能用複數解。

補充一下，點D就是點O

打錯了

補充一道題：
(5)若正方形A'B'C'O的對角線交於點P'，求P'的坐標

這沒必要扯上複數吧，用用向量就行了

——yaoliding

這題應該就是初中水平