【动画】在四维空间旋转三维轮胎 [圖片] |
回覆:关于三维球面的横截面还有,标题打错了,是“关于四维超球的横截面”
|
回覆:关于三维球面的横截面三维球面分布着经面和纬面,而二维球面是经线和纬线
|
回覆:关于三维球面的横截面在圆的边界上(即一维球面S1),向前或向后走能回到起点。
在三维球体的表面上(即二维球面S2),向上、下、左、右走都能回到起点。 那么,在三维球面S3上,就有六个正方向可以回到起点。... |
回覆:关于三维球面的横截面也就是这样:http://zh.arslanbar.net/post.php?i=25384
|
关于三维球面的横截面二维的圆,可以由无数个从短到长,再到短的直线拼成
三维的球,可以有从小到大,再到小的二维圆拼成 那么,四维的球就是从小到大,再到小的三维球体拼成了 |
回覆:请 吧主进来 帮我解决个问题所有的四维物体,表面是三维的。
但最后一句说实话我也看不懂,因为不是我写的 |
这个图不会就是四维轮胎吧? [圖片] |
请 吧主进来 帮我解决个问题正多胞体定义:
它是一个四维空间上的多胞形(Polytope,点、线段、多边形、多面体,以及更高维度的几何物体的总称) 多胞体表面(Facet)由有限个正多面体组成,每个顶点情况相... |
一道四维单形的证明题 [圖片]任意五胞体EABCD自五个顶点分别引出四条直线(每个顶点不同颜色)使得自这一顶点引出的四条直线所组成的五胞体的各侧四面体所成二胞角分别为以
这一点为顶点对应的原五胞体EABCD各侧四面体所成二胞角的3...
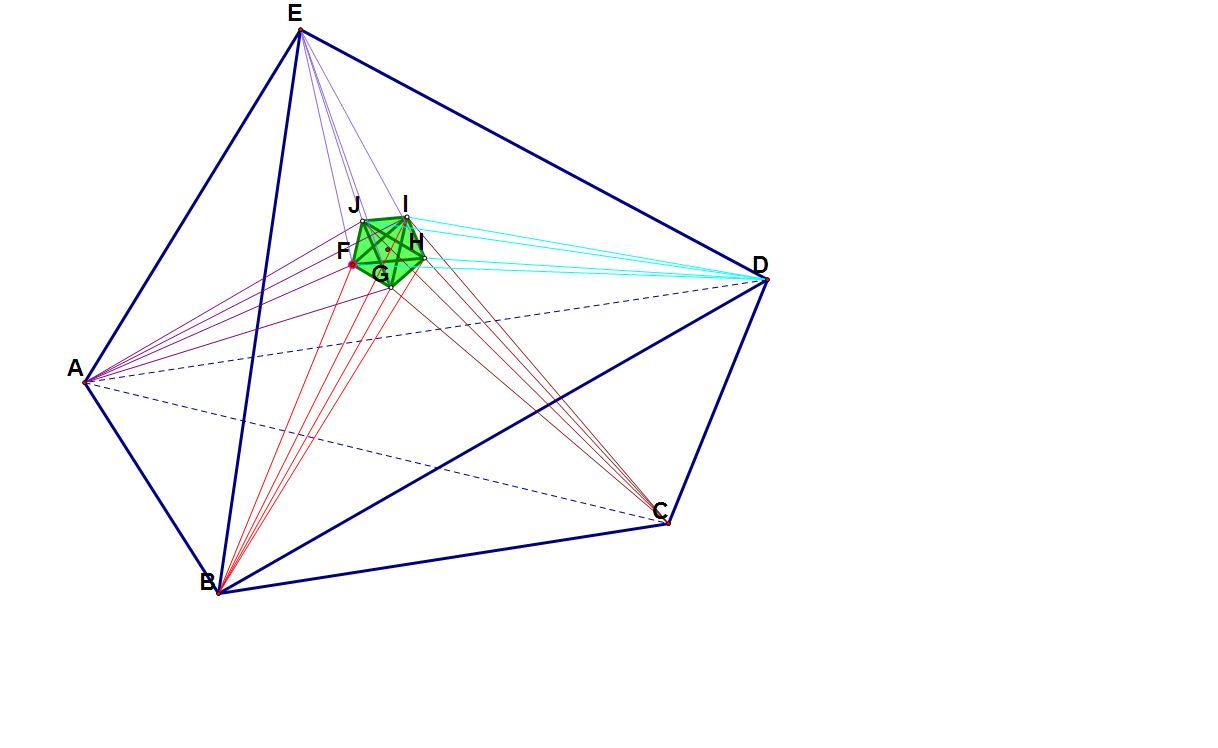 |