通过五维单形的球极投影,可以数出有6个顶点 [圖片] |
【个人认为】4D文字和超正方体的推倒差不多就是把3D文字复制一份,然后连接各个顶点
|
【调查一下】各位都是几年级的 [投票] |
关于三维球面的横截面二维的圆,可以由无数个从短到长,再到短的直线拼成
三维的球,可以有从小到大,再到小的二维圆拼成 那么,四维的球就是从小到大,再到小的三维球体拼成了 |
各种正多胞体的三维类比5-cell:四面体
8-cell:正方体 16-cell:八面体 24-cell:无 120-cell:十二面体 600-cell:二十面体 |
【flash】1-4维的正方体 |
2011年4月21日
64.34.204.*
4-21
64.34.204.*
(點擊/回復: 659/1)
|
超正方体的体积计算公式V4=a^4
218.88.141.*
4-19
4Der
(點擊/回復: 857/5)
|
貌似施莱格尔投影和球极投影都不是物体的原型用手电筒照一个四维物体叫什么投影?
4Der
4-18
219.137.36.*
(點擊/回復: 748/1)
|
这些是不是多胞体的展开图 [圖片]24cell:
 |
话说我认为多维图形的二维线架图很像分形的说并且维数越高分形图形越精细
|
【问题】五维单形大概有多少个四维单形?rt
|
【图片】正多胞体的三维展开图http://zh.arslanbar.net/pictures.php?b=%E5%9B%9B%E7%BB%B4%E5%87%A0%E4%BD%95%E5%AD%A6&label=album...
|
ubuntu11.04也没几天就发布了rt
|
前十维基本多胞形表格,看的懂的求陪同 [圖片]我写的
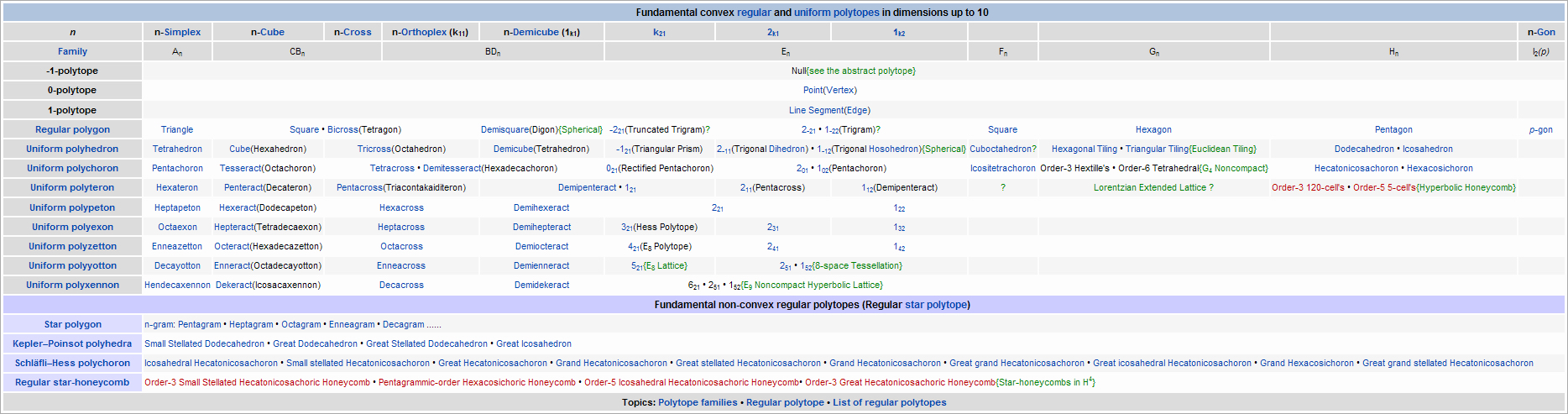 |
| 全站共有主題數31560個,帖子數145537篇。 |
內容轉換: |