参考：https://www-sop.inria.fr/cafe/Manuel.Bronstein/publications/issac98.pdf

计算机如何自动计算不定积分，是一个长期感兴趣的问题，1968年出现的Risch算法，以及在1976年的改进Risch–Norman算法在相当程度上解决了这个问题，这些算法可以自动求解初等函数的不定积分，前提是积分也是初等函数。

第一种情况，有理函数的积分。
有理函数是两个多项式的商。根据代数基本定理，多项式一定能在代数闭域内分解为一次多项式的乘积，而在实数域内，则分解成一次多项式和判别式为负数的二次多项式的乘积：

如果上述D是有理函数的分母，那么通过所谓部分分式展开，可以把有理函数写成下列形式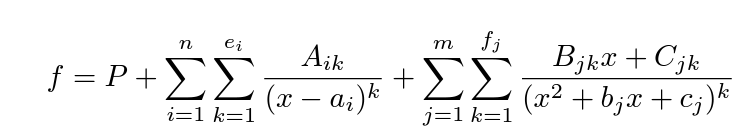


其中P是多项式，Aik,Bjk,Cjk,ai,bj,cj都是实数。
那么，要计算这个积分，只需要分别计算每一项的积分即可。多项式P的积分容易计算；其余各项的积分如下：

1. 分母为一次式的k次方：2. 分母为二次式，k=1：
这里的判别式4cj-bj^2<0.

3. 分母为二次式，k>1：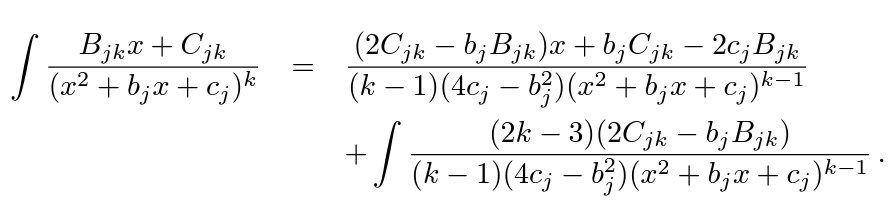
这样就可以递推式地降低k，直到k=1.

这种算法有一个重大缺陷：并没有什么算法可以得到所需的因式分解。这并不是说因式分解不存在，而是我们无法通过一种算法求解它。例如，五次方程x^5-x+1=0就没有根式解。（即使通过特殊函数，也会涉及希尔伯特第十三问题而难以解决）

为了解决这个问题，我们首先需要对分母的因式分解进行限制，保证其有相应的算法。

如果多项式f有不可约因式g^m, 但g^{m+1}不是f的因式，那么f和f导数f'的公因式(f,f')能被g^{m-1}整除，但不能被g^m整除。

我们用这个事实，可以得知公因式h=(f,f')的每个不可约因式的次数比f小1.

我们假设f是首一多项式，把相同重数的不可约因式放在一起，设

那么，首一公因式(f,f')为

于是，我们有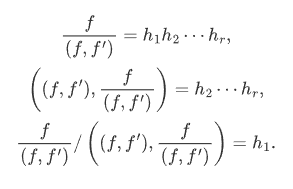

也就是说，我们不难从f求出无重数部分h1. 进而，可以再对(f,f')使用该算法求出h2,等等。因此，我们的算法最终可以把f的上述分解（也就是对应于每个重数的h1,h2....,hr）求出来。

上述算法成功把分母的最高重数从m降到了m-1，因此重复上述步骤，就可以把有理积分化约为分母无平方因子的情况。这叫做厄尔米特约化（Hermite reduction）。

根据厄尔米特约化，我们只需要求A/D, deg(A)<deg(D), D无平方因子，这种情况的不定积分。
我们考虑在复数域内对D进行分解，结果是互不相同（因为D无平方因子）的单项式的乘积，因此A/D有部分分式展开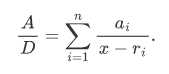

此时，使用复对数，可以把积分表示为

其中C是任意常数。当然，我们是不会满足于这种表示的，因为它很明显仍然没有规避高次方程求根的问题。

这里的ai显然等于A/D在单极点ri的留数。设D=D1(x-ri), 那么不难计算出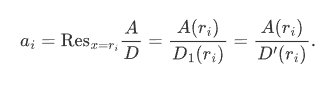

因此，ri是D和A-aiD'的公共零点。根据结式（https://zh.wikipedia.org/wiki/%E7%B5%90%E5%BC%8F）的性质，ai恰好就是结式

的根（即使得上述结式等于零的t）。

如果R的不可约分解为

那么我们可以求出不定积分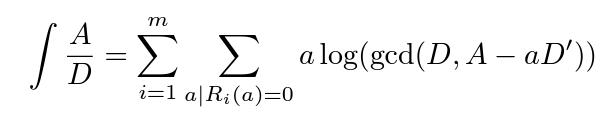很明显，这个结果并非完美。我们仍然需要使用Ri的根来表示这个结果，而不可约多项式Ri仍然可能是高次的不可求根式解的多项式。但已经证明，要把这个不定积分表示成初等函数，我们至少需要在R在K上的分裂域上表示。因此，这个结果理论上已经是最简化的。

但是上述算法仍然可以改进。实际上，我们不需要直接对R进行不可约分解，先进行无平方因子分解也是可以的：

我们有

其中pp是指多项式的“本原部分”，也就是多项式乘以一个适当的数以后，得到的以互素整元素为系数的新多项式。Rki是所谓“子结式”。两个多项式的子结式是以它们的结式开始的，一系列以它们的系数为变量的，次数递减的多元多项式，其满足的性质是：两个多项式有k个公共零点，当且仅当其前k个子结式为零。

这个结果还是不可避免地出现了一些无法求出的高次方程的根，但我们已经可以基本上仅仅用它们表示结果而不是对它们进行实际计算。即使是对本原部分（pp）的计算，也是可以避免的，参考T. Mulders. A note on subresultants and a correction to the LazardRioboo–Trager formula in rational function integration. Journal of Symbolic Computation, 24(1):45–50, 1997.

第二种情况，代数函数的积分。

设K是一个数域，K上的一个代数函数是指K(x)的一个有限生成的代数扩张E中的一个元素。
代数函数可能可以用根式表示，例如

但也有很多代数函数并不能写成根式形式。此时，我们只能用隐函数表示这个代数函数。具体来说，设

是E中的元素，由于E是K(x)的代数扩张，所以我们总可以找到多项式

这样，alpha就可以看成是x的隐函数。