參考：https://www-sop.inria.fr/cafe/Manuel.Bronstein/publications/issac98.pdf

計算機如何自動計算不定積分，是一個長期感興趣的問題，1968年出現的Risch算法，以及在1976年的改進Risch–Norman算法在相當程度上解決了這個問題，這些算法可以自動求解初等函數的不定積分，前提是積分也是初等函數。

第一種情況，有理函數的積分。
有理函數是兩個多項式的商。根據代數基本定理，多項式一定能在代數閉域內分解為一次多項式的乘積，而在實數域內，則分解成一次多項式和判別式為負數的二次多項式的乘積：

如果上述D是有理函數的分母，那麼通過所謂部分分式展開，可以把有理函數寫成下列形式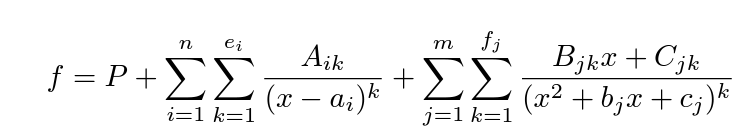


其中P是多項式，Aik,Bjk,Cjk,ai,bj,cj都是實數。
那麼，要計算這個積分，只需要分別計算每一項的積分即可。多項式P的積分容易計算；其餘各項的積分如下：

1. 分母為一次式的k次方：2. 分母為二次式，k=1：
這裏的判別式4cj-bj^2<0.

3. 分母為二次式，k>1：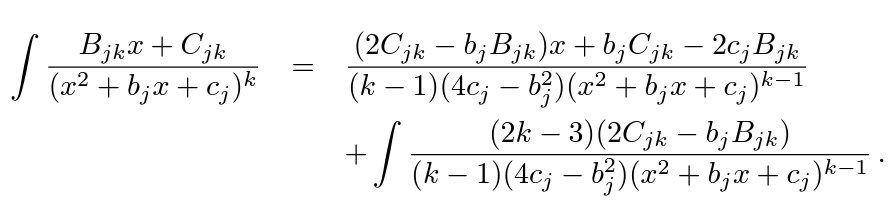
這樣就可以遞推式地降低k，直到k=1.

這種算法有一個重大缺陷：並沒有什麼算法可以得到所需的因式分解。這並不是說因式分解不存在，而是我們無法通過一種算法求解它。例如，五次方程x^5-x+1=0就沒有根式解。（即使通過特殊函數，也會涉及希爾伯特第十三問題而難以解決）

為了解決這個問題，我們首先需要對分母的因式分解進行限制，保證其有相應的算法。

如果多項式f有不可約因式g^m, 但g^{m+1}不是f的因式，那麼f和f導數f'的公因式(f,f')能被g^{m-1}整除，但不能被g^m整除。

我們用這個事實，可以得知公因式h=(f,f')的每個不可約因式的次數比f小1.

我們假設f是首一多項式，把相同重數的不可約因式放在一起，設

那麼，首一公因式(f,f')為

於是，我們有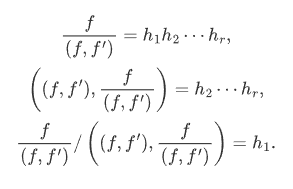

也就是說，我們不難從f求出無重數部分h1. 進而，可以再對(f,f')使用該算法求出h2,等等。因此，我們的算法最終可以把f的上述分解（也就是對應於每個重數的h1,h2....,hr）求出來。

上述算法成功把分母的最高重數從m降到了m-1，因此重複上述步驟，就可以把有理積分化約為分母無平方因子的情況。這叫做厄爾米特約化（Hermite reduction）。

根據厄爾米特約化，我們只需要求A/D, deg(A)<deg(D), D無平方因子，這種情況的不定積分。
我們考慮在複數域內對D進行分解，結果是互不相同（因為D無平方因子）的單項式的乘積，因此A/D有部分分式展開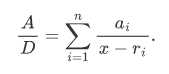

此時，使用複對數，可以把積分表示為

其中C是任意常數。當然，我們是不會滿足於這種表示的，因為它很明顯仍然沒有規避高次方程求根的問題。

這裏的ai顯然等於A/D在單極點ri的留數。設D=D1(x-ri), 那麼不難計算出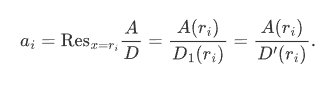

因此，ri是D和A-aiD'的公共零點。根據結式（https://zh.wikipedia.org/wiki/%E7%B5%90%E5%BC%8F）的性質，ai恰好就是結式

的根（即使得上述結式等於零的t）。

如果R的不可約分解為

那麼我們可以求出不定積分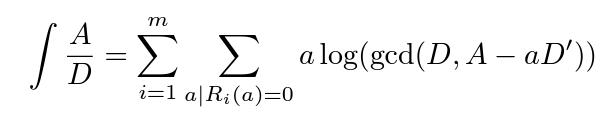很明顯，這個結果並非完美。我們仍然需要使用Ri的根來表示這個結果，而不可約多項式Ri仍然可能是高次的不可求根式解的多項式。但已經證明，要把這個不定積分表示成初等函數，我們至少需要在R在K上的分裂域上表示。因此，這個結果理論上已經是最簡化的。

但是上述算法仍然可以改進。實際上，我們不需要直接對R進行不可約分解，先進行無平方因子分解也是可以的：

我們有

其中pp是指多項式的「本原部分」，也就是多項式乘以一個適當的數以後，得到的以互素整元素為係數的新多項式。Rki是所謂「子結式」。兩個多項式的子結式是以它們的結式開始的，一系列以它們的係數為變量的，次數遞減的多元多項式，其滿足的性質是：兩個多項式有k個公共零點，當且僅當其前k個子結式為零。

這個結果還是不可避免地出現了一些無法求出的高次方程的根，但我們已經可以基本上僅僅用它們表示結果而不是對它們進行實際計算。即使是對本原部分（pp）的計算，也是可以避免的，參考T. Mulders. A note on subresultants and a correction to the LazardRioboo–Trager formula in rational function integration. Journal of Symbolic Computation, 24(1):45–50, 1997.

第二種情況，代數函數的積分。

設K是一個數域，K上的一個代數函數是指K(x)的一個有限生成的代數擴張E中的一個元素。
代數函數可能可以用根式表示，例如

但也有很多代數函數並不能寫成根式形式。此時，我們只能用隱函數表示這個代數函數。具體來說，設

是E中的元素，由於E是K(x)的代數擴張，所以我們總可以找到多項式

這樣，alpha就可以看成是x的隱函數。