回复:【百度百科】超正方体
3-12
·
超正方体Tesseract的施莱夫利符号有几个
{4,3,3}(特指它是正多胞体Tesseract); {4,3}x{}(代指Cubic prism); {4}x{4}(4-4 duoprism,由两个正方形绝对垂直得到); {4}x{}x{}(代指Square prismatic prism,就是一个正方形柱——通俗的说还是立方体——的柱形); {}x{}x{}x{}(代指Line segmentary prismatic prismatic prism,... |
||
回复:【百度百科】超正方体
3-12
·
零维的一个点,包含一个零维元素(点);一维的一条线段,包含一个一维元素(线段),两个零维元素;二维的一个正方形,包含一个二维元素(面),四个一维元素;三维的一个正方体,包含 一个三维元素(三维立体),六个二维元素,十二个一维元素,八个零维元素
对比下列算式: (x+2)^0=1 (x+2)^1=x+2 (x+2)^2=x^2+4x+4 (x+2)^3=x^3+6x^2+12x+8 可以归纳出:一个n维立方形(n-cube)所包含的k... |
||
回复:【百度百科】超正方体 [图片]
3-12
·
大家一定知道把立方体的六个面展开的样子吧,其中一种展开法如右图。
类比一下,即可得到超正方体的其中一种展开法,如最右图,其中一个立方体被藏在三维展开图里边了。 看上去很奇怪是吧,这八个立方体在我们的世界里无论怎么翻转也不能组成一个超正方体的,它们必须在四维空间里旋转——这个比方就好比二维小人不会明白那六个正方形怎么转才能拼成一个立方体一样的道理。 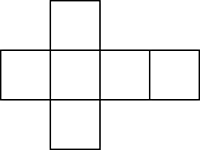 
|
||
回复:【百度百科】超正方体 [图片]
3-12
·
思维方式
如果四维超正方体不太好想象的话,我们换成球试试吧。三维球嘛,无论从哪个方向投影在二维平面上都只是一个半经等同的圆形,这样我们就很容易想到四维球在三维世界中的投影只不过是一个半径等同的球了。如果还想要讨论得深入一些,不妨试试球穿越问题。比如说一个球穿过一个二维平面,二维小人会发现平面上凭空冒出一个慢慢变大的点,后来眼看着扩张成圆,又慢慢缩小成点,最后突然消失。如果这个令二维小人惊讶不已的事实让你并不觉得奇怪,那么以下的情形你定会吃惊不小;在你面前无中生有地出现一个点,扩...  
|
||
回复:【百度百科】超正方体 [图片]
3-12
·
施莱格尔投影
四维方体不易想象,但可以投射至3维或2维空间。在2维平面的投射,把顶点位置调整后,可以了解更多。如此获得的图像,不再反映四维方体空间构造,而是反映顶点间的联系。 对于生活在三维空间的人类来说,四维世界是很神秘的概念。正像生活在二维世界里的小人(如果存在)很难想象三维世界一样,我们同样难于想象四维世界。不过也正像我们可以通过研究三维物体在二维物体上的投影来研究想象三维物体一样,我们也可以通过四维物体在三维世界中的立体图形投影来研究四维世界。... 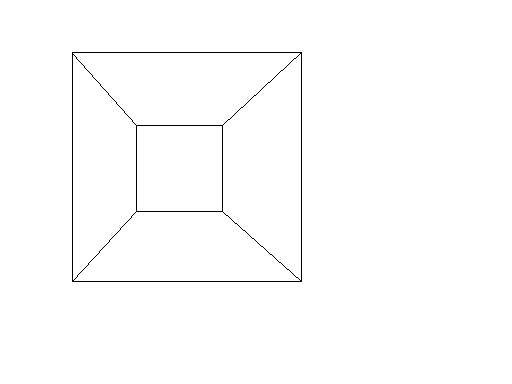 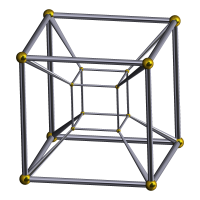
|
||
回复:【百度百科】超正方体
3-12
·
超立方体,又作正八胞体(8-cell,Regular octachoron),立方体柱(Cubic prism),4-4边形柱(4-4 duoprism),是一个四维空间里的几何产物
需要说一下“超立方体”的英文应该是Tesseract而不是Hypercube,Hypercube在英文维基百科上是指N维立方体(一维的线段,二维的正方形,三维的立方体……)的总称 |
||
【百度百科】超正方体 [图片]
3-12
·
超正方体(Tesseract, hypercube)又称超立方体或正八胞体,在几何学中四维方体是立方体的四维类比,四维方体之于立方体,就如立方体之于正方形,四维方体是四维凸正多胞体,有8个立方体胞,立方体维数大于3推广的是超立方体或测度多胞体。

|
||
回复:超正方体 [图片]
3-12
·

|
||
超正方体
3-12
·
超正方体(Tesseract,hypercube)又称超立方体或正八胞体,在几何学中四维方体是立方体的四维类比,四维方体之于立方体,就如立方体之于正方形,四维方体是四维凸正多胞体,有8个立方体胞,立方体维数大于3推广的是超立方体或测度多胞体。 超立方体存在于四维空间之中,我们所谓的点动成线,线动成面,面动成体。在加入时间轴的概念之中,立方体的移动形成四维的超立方体,由无数个立方体所组成的,具有四维的观念。在超立方体中可以理解为时间作为一个盒子包裹在一个三维空间之中。
然 而,所谓的四维空间... |
||
您好,阿斯兰侃吧欢迎您的到来~
3-12
·
亲爱的用户:欢迎来到四维几何学吧,阿斯兰侃吧欢迎您的到来~
请先阅读我们的社区准则:http://documents.arslanbar.net/eula/zh/ 以及版权声明:http://documents.arslanbar.net/copyright/zh/ 您可在此畅所欲言,并和朋友们交流~~ 祝您在此吧玩得愉快~ 侃吧管理员 |
||