| 點擊 |
回復 |
標題 |
作者 |
最後回復 |
| 976 |
2 |
因为球极投影后是四维,再平行投影就乱七八糟了
|
魔法绿骑士 |
5-7 魔法绿骑士 |
| 1052 |
1 |
如图,已知四边形ABCO是正方形,O是原点。点E为AB的中点。连接AC、BO,交于点F,且C点的坐标为(7,1)。 (1)...  |
魔法绿骑士 |
5-7 yaoliding |
| 3398 |
11 |
octopus@phpServer:~$ cd 下载
octopus@phpServer:~/下载$ tgz zxvf jenn3d.2008_01_15.tgz
Writing gzip...
|
4Der |
5-2 125.67.191.* |
| 1075 |
7 |
|
魔法绿骑士 |
5-2 125.67.191.* |
| 1172 |
6 |
|
魔法绿骑士 |
4-30 yaoliding |
| 930 |
2 |
上面三个小,下面那个大
|
魔法绿骑士 |
4-30 yaoliding |
| 951 |
1 |
比正多胞体好理解得多
|
魔法绿骑士 |
4-29 yaoliding |
| 1183 |
7 |
先看看在二维的纸上画三维的正四面体。先画四个点,然后每个点两两相连,共画六条棱。 画出来后发现有两条棱相交了,但实际上根本没有相交。并且,后面的那条横着的棱被两个面挡住了,所以画成虚线。... 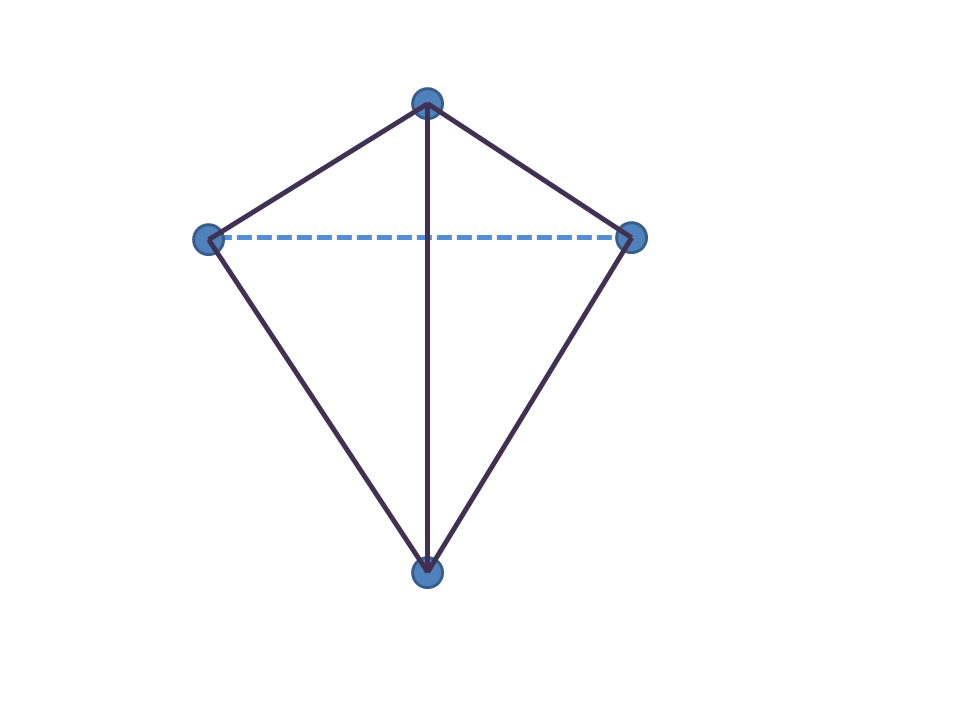 |
4Der |
4-29 yaoliding |
| 2019 |
12 |
爱因斯坦说:四维?有啊,时间就是第四维 扯他的蛋去吧。我这里将要说的四维空间,是指纯几何意义上的思维。 在两百年以前,人们普遍认为数学是一种工具,是要为现实服务的。...  |
魔法绿骑士 |
4-27 魔法绿骑士 |
| 1056 |
2 |
http://www.polytope.de/
这是网站首页
http://www.polytope.de/c5.html#bild1
这是正五胞体
|
魔法绿骑士 |
4-24 yaoliding |
| 986 |
1 |
|
魔法绿骑士 |
4-24 yaoliding |
| 913 |
1 |
600-cell  |
魔法绿骑士 |
4-24 魔法绿骑士 |
| 1052 |
1 |
呼
|
yaoliding |
4-24 4Der |
| 953 |
2 |
-i-1=(-1,-1)
设根号(-1,-1)=(x,y)
则
x²-y²=-1
2xy=-1
|
4Der |
4-23 yaoliding |
| 926 |
9 |
上次说到维度时,有人提到了如何理解四维空间的问题。这是一个非常有趣的话题,可是我一直没有用心写一下。前段时间网上出了一部片子叫做Dimensions: a walk through mathemati...
|
4Der |
4-23 118.117.5.* |
| 973 |
5 |
线:2×(12+4+6×4)+(8+1+6)=95
和影片不符啊,我少算了哪条线?
|
4Der |
4-22 yaoliding |
| 884 |
0 |
rt
|
4Der |
4-22 4Der |
| 860 |
4 |
若把四维球体球极投影到三维空间,就会占满整个三维空间(。。。)!
|
4Der |
4-22 4Der |
| 1107 |
5 |
rt
|
4Der |
4-22 yaoliding |
| 735 |
0 |
维度 全称 简称
0 零维面 点
1 一维面 线或棱
2 二维面 面
3...
|
4Der |
4-22 4Der |
| 753 |
0 |
也就是四维空间中的普通黑板,其表面是三维,所以能画三维图形
|
4Der |
4-22 4Der |
| 1020 |
4 |
我要类比学习四维星形多胞体
|
4Der |
4-22 yaoliding |
| 1011 |
9 |
平行投影严重破坏了120胞体的形态,导致各个正12面体互相相交,分不清谁是谁。
但球极投影后,各个12面体就挨个挨个的摆在一起,没有重合,很容易分辨。
当然超正方体也是一样的,直接看平行投...
|
4Der |
4-22 yaoliding |
| 1050 |
2 |
一个贴的内容太简单了,我觉得不如集中到一个贴里有想说的话的时候留个言
我希望这吧可以像四维空间吧那么多一点人去讨论一下
|
yaoliding |
4-22 yaoliding |
| 1173 |
6 |
在二维空间中,我们给蜥蜴几个三维球体的横截面——即各种大小不同的圆,让蜥蜴在二维空间去拼三维球体,结果二维空间的蜥蜴根本拼不出来,他只是把各个圆摆在了一起,没有拼成真正的球体。
我们也一样,给我...
|
4Der |
4-22 yaoliding |
| 889 |
2 |
就好比四维生物在三维平面上画正五胞体
|
4Der |
4-22 yaoliding |
| 828 |
2 |
rt
|
4Der |
4-22 yaoliding |
| 917 |
1 |
任意五胞体EABCD自五个顶点分别引出四条直线(每个顶点不同颜色)使得自这一顶点引出的四条直线所组成的五胞体的各侧四面体所成二胞角分别为以
这一点为顶点对应的原五胞体EABCD各侧四面体所成二胞角的3... 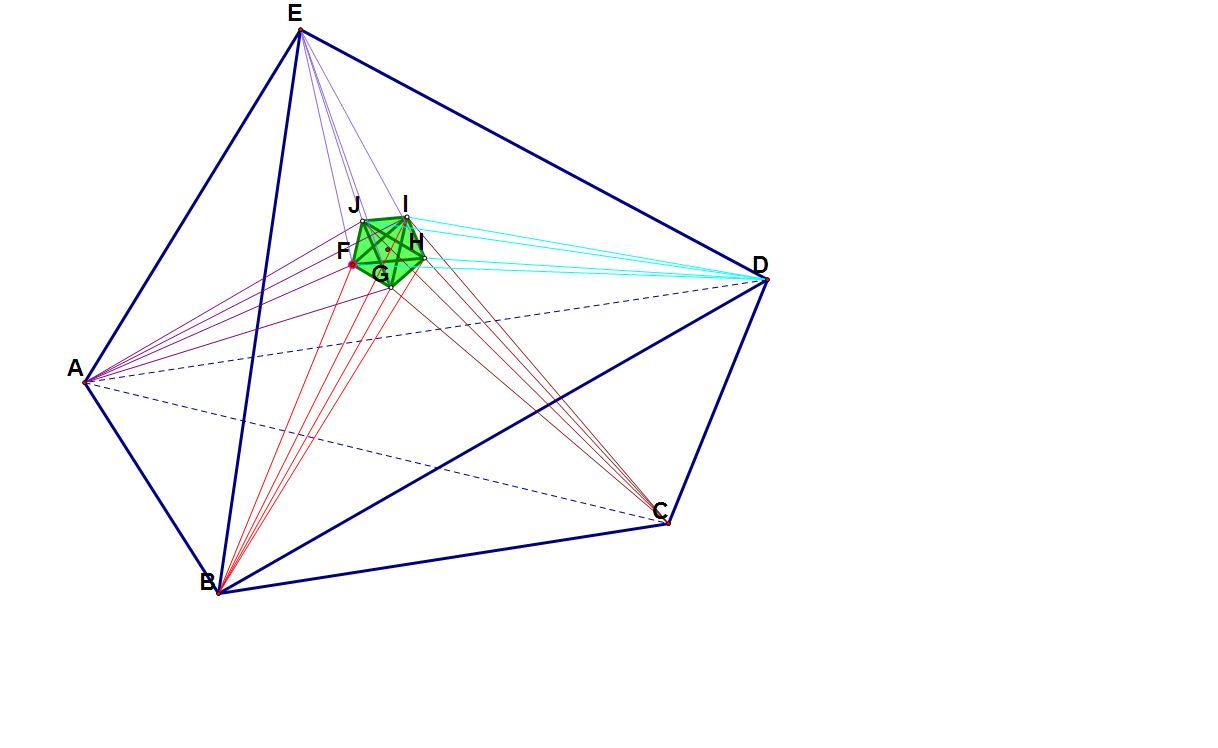 |
4Der |
4-22 yaoliding |
| 981 |
1 |
|
4Der |
4-22 yaoliding |
| 1047 |
2 |
正多胞体定义:
它是一个四维空间上的多胞形(Polytope,点、线段、多边形、多面体,以及更高维度的几何物体的总称)
多胞体表面(Facet)由有限个正多面体组成,每个顶点情况相...
|
695223183 |
4-22 yaoliding |
| 898 |
1 |
|
4Der |
4-22 yaoliding |
| 980 |
2 |
就是把3D文字复制一份,然后连接各个顶点
|
4Der |
4-22 yaoliding |
| 1084 |
4 |
|
4Der |
4-22 yaoliding |
| 921 |
5 |
二维的圆,可以由无数个从短到长,再到短的直线拼成
三维的球,可以有从小到大,再到小的二维圆拼成
那么,四维的球就是从小到大,再到小的三维球体拼成了
|
4Der |
4-22 yaoliding |
| 804 |
1 |
5-cell:四面体
8-cell:正方体
16-cell:八面体
24-cell:无
120-cell:十二面体
600-cell:二十面体
|
4Der |
4-22 yaoliding |
| 856 |
1 |
|
4Der |
4-21 4Der |
| 847 |
5 |
V4=a^4
|
218.88.141.* |
4-19 4Der |
| 739 |
1 |
用手电筒照一个四维物体叫什么投影?
|
4Der |
4-18 219.137.36.* |
| 959 |
3 |
24cell:  |
4Der |
4-17 yaoliding |
| 890 |
1 |
并且维数越高分形图形越精细
|
4Der |
4-17 yaoliding |
| 817 |
1 |
rt
|
4Der |
4-17 yaoliding |
| 748 |
0 |
http://zh.arslanbar.net/pictures.php?b=%E5%9B%9B%E7%BB%B4%E5%87%A0%E4%BD%95%E5%AD%A6&label=album...
|
4Der |
4-17 4Der |
| 955 |
4 |
我写的 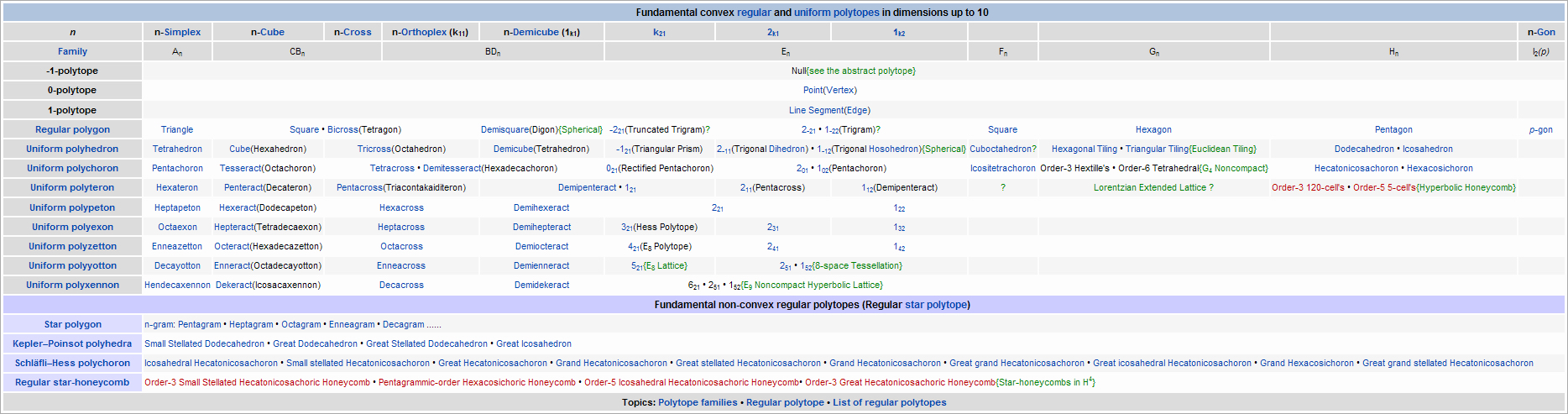 |
yaoliding |
4-17 4Der |
| 898 |
3 |
rt
|
4Der |
4-17 yaoliding |
| 743 |
0 |
不仅仅是超球
|
4Der |
4-17 4Der |
| 1025 |
5 |
http://zh.arslanbar.net/post.php?i=12737
你看,某人灌了那么多,都没被封过
但如果是百度那就不一样了,灌到200多层就会删帖+系统自动永久封禁...
|
4Der |
4-16 yaoliding |
| 877 |
1 |
但三维平面就很难想像了,因为涉及到四维空间
|
4Der |
4-16 yaoliding |
| 793 |
2 |
【资料】正多胞体 [高维基础] [置顶]
意思是说这个帖子是精品贴,所属分类为“高维基础”。此时“高维基础”这四个字是淡蓝色
|
4Der |
4-16 4Der |
| 851 |
4 |
rt
|
4Der |
4-16 4Der |
| 892 |
4 |
那些正多胞体也是扩充成球后进行球极投影的,为何不填满整个三维空间?
|
4Der |
4-16 yaoliding |