【一道题】正方形坐标题 [圖片]如图,已知四边形ABCO是正方形,O是原点。点E为AB的中点。连接AC、BO,交于点F,且C点的坐标为(7,1)。
(1)...  |
我在jenn中弄出了12面体 [圖片]
魔法绿骑士
5-2
125.67.191.*
(點擊/回復: 1078/7)
|
【动画】在四维空间中旋转三维正方体 [圖片] |
【图片】在三维空间中画正五胞体 [圖片]先看看在二维的纸上画三维的正四面体。先画四个点,然后每个点两两相连,共画六条棱。
画出来后发现有两条棱相交了,但实际上根本没有相交。并且,后面的那条横着的棱被两个面挡住了,所以画成虚线。... 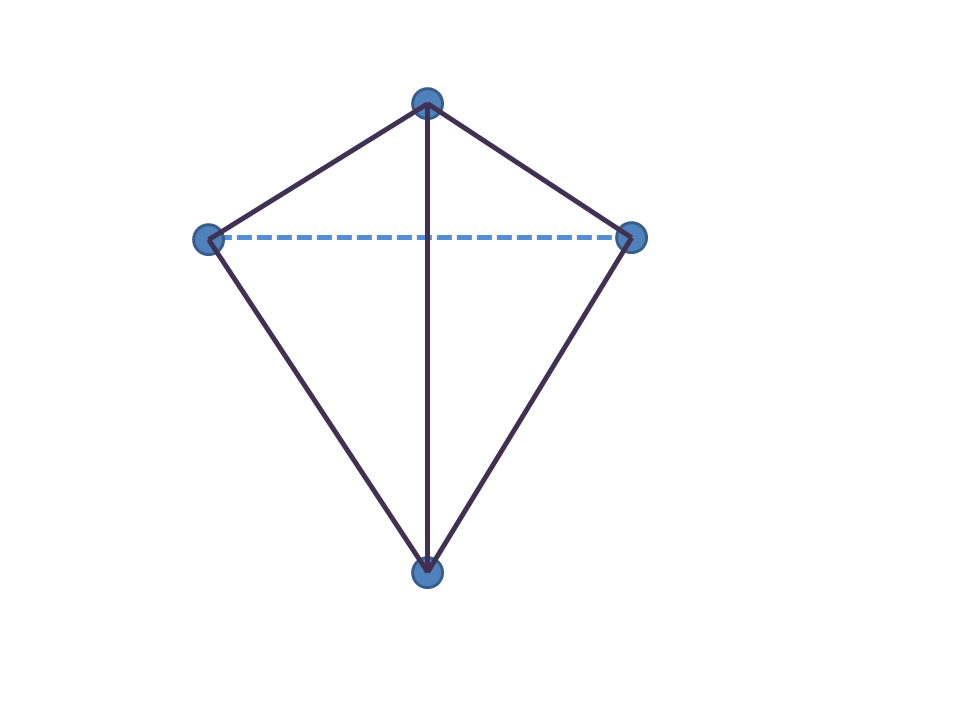 |
【转载】【科普向】教你观察和想象四维空间 [圖片]爱因斯坦说:四维?有啊,时间就是第四维
扯他的蛋去吧。我这里将要说的四维空间,是指纯几何意义上的思维。 在两百年以前,人们普遍认为数学是一种工具,是要为现实服务的。...  |
【图片】三维多面体的施莱格尔投影 [圖片] |
【图片】正多胞体的旋转图 [圖片]600-cell
 |
一道四维单形的证明题 [圖片]任意五胞体EABCD自五个顶点分别引出四条直线(每个顶点不同颜色)使得自这一顶点引出的四条直线所组成的五胞体的各侧四面体所成二胞角分别为以
这一点为顶点对应的原五胞体EABCD各侧四面体所成二胞角的3...
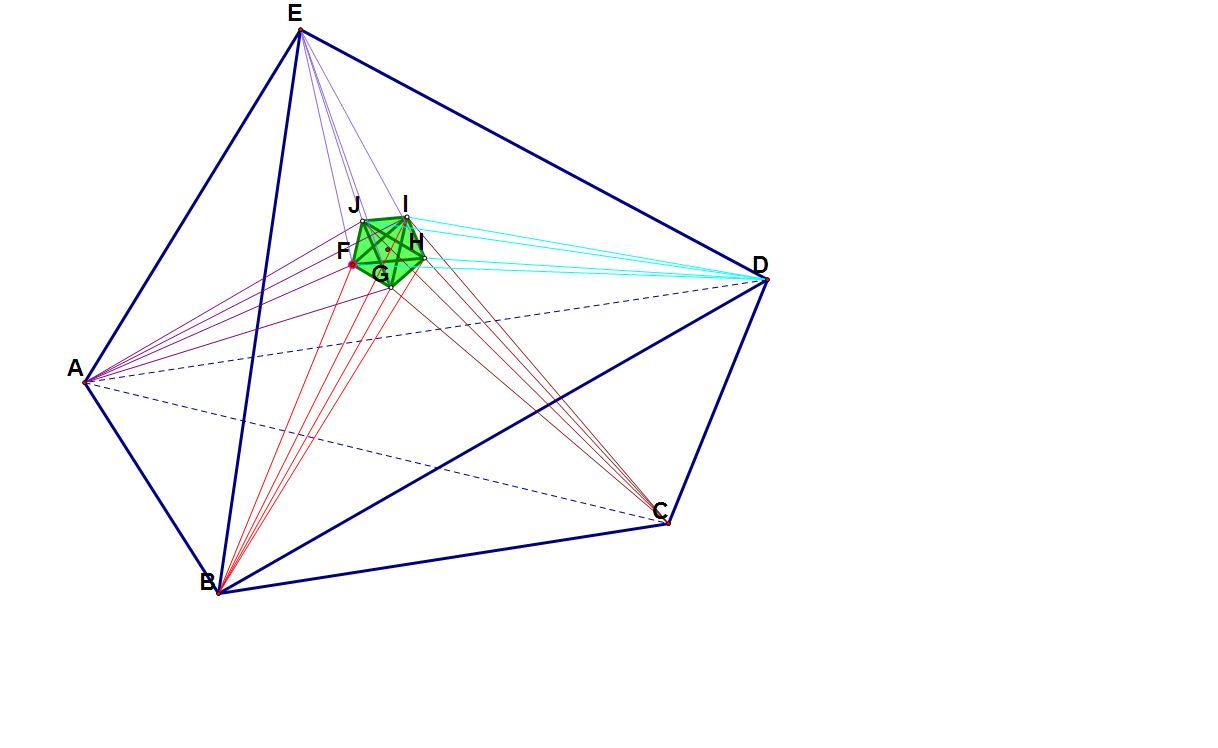 |
这个图不会就是四维轮胎吧? [圖片] |
通过五维单形的球极投影,可以数出有6个顶点 [圖片] |
这些是不是多胞体的展开图 [圖片]24cell:
 |
前十维基本多胞形表格,看的懂的求陪同 [圖片]我写的
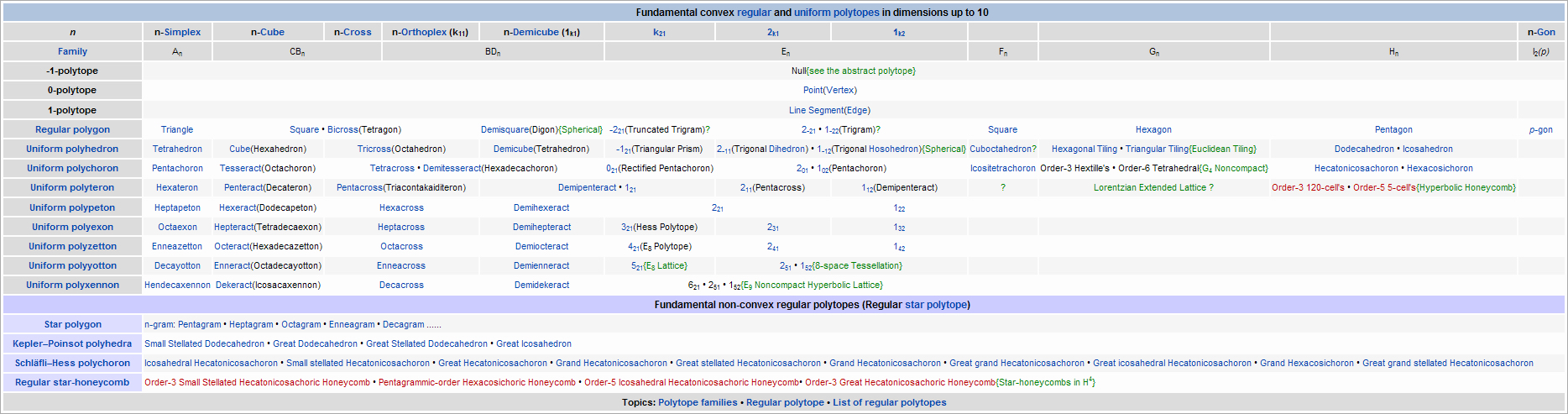 |
jenn中滚动球极投影 [圖片]这是影片中的8-cell第二种类型的球极投影滚动动画中的一幕:
时间大约是5:39  |
【转载】Fundamental convex & non-convex uniform po [高维基础] [圖片]写这个估计没人懂的了,我自娱自乐好了
顺便BS一下百度相册,最长边最多只有1600像素,干脆用网易好了 再BS一下,bmp图居然不能点击看大图 一个我在英文wiki上自己改的Poly...  |
【图片】jenn3d也可以进行球极投影滚动 [圖片] |
| 本吧共有33篇圖片帖。 |
內容轉換: |