一元四次方程的求根公式主要有兩種。
第一種是用y=u+v+w推導出來的只含三層根號的公式，形式為x=-b/4a±1√L±2√M±3√N，其中L、M、N是某三次方程的三根。公式中的分母只含a，不含其它任何字母，可以求解任意四次方程。但公式中含有虛數ω，計算比較繁瑣。
第二種是用配平方法、待定係數法等方法推導出來的含有四層根號的公式。公式中不含虛數，但是分母中含有a以外的字母，當q=0時無法利用這些求根公式求解。
這裡我們選擇第一種公式求解。

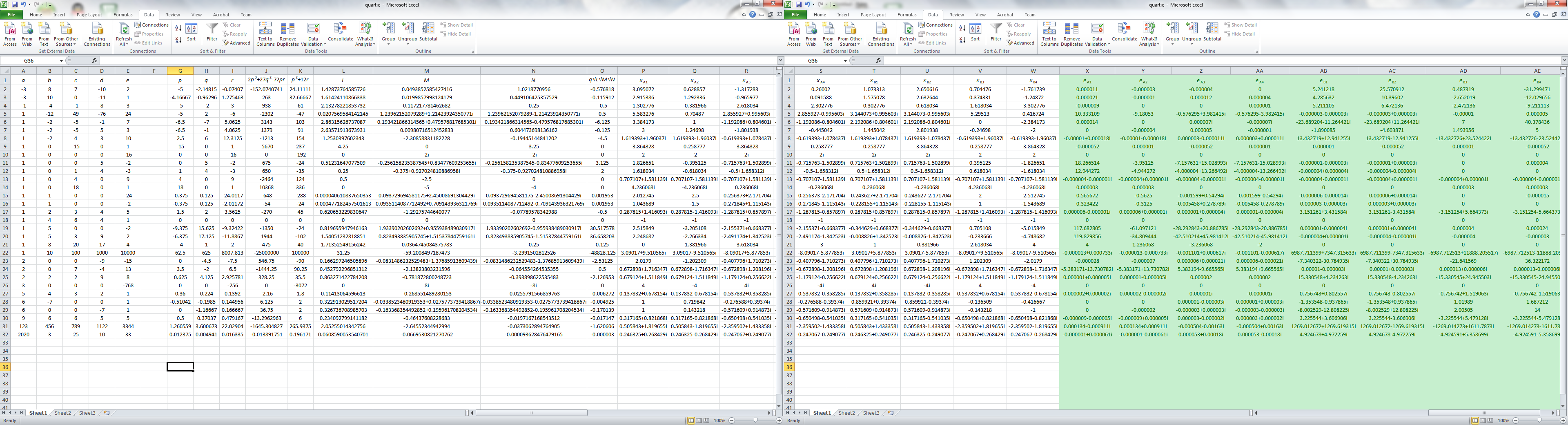
A~E欄填寫方程的係數（實數）
G欄計算參數p：
=(8*A2*C2-3*B2*B2)/(8*A2*A2)
H欄計算參數q：
=(8*A2*A2*D2-4*A2*B2*C2+B2*B2*B2)/(8*A2*A2*A2)
I欄計算參數r：
=(256*A2*A2*A2*E2-64*A2*A2*B2*D2+16*A2*B2*B2*C2-3*B2*B2*B2*B2)/(256*A2*A2*A2*A2)
J欄計算2p³+27q²-72pr：
=2*G2*G2*G2+27*H2*H2-72*G2*I2
K欄計算p²+12r：
=G2*G2+12*I2
L欄計算參數L：
=IMDIV(IMSUM(-2*G2,IMCBRT(IMDIV(IMSUM(J2,IMSQRT(J2*J2-4*K2*K2*K2)),2)),IMCBRT(IMDIV(IMSUB(J2,IMSQRT(J2*J2-4*K2*K2*K2)),2))),12)
M欄計算參數M：
=IMDIV(IMSUM(-2*G2,IMCBRT(IMDIV(IMSUM(J2,IMSQRT(J2*J2-4*K2*K2*K2)),2),1),IMCBRT(IMDIV(IMSUB(J2,IMSQRT(J2*J2-4*K2*K2*K2)),2),2)),12)
N欄計算參數N：
=IMDIV(IMSUM(-2*G2,IMCBRT(IMDIV(IMSUM(J2,IMSQRT(J2*J2-4*K2*K2*K2)),2),2),IMCBRT(IMDIV(IMSUB(J2,IMSQRT(J2*J2-4*K2*K2*K2)),2),1)),12)
O欄為q√L√M√N的值，用來判斷方程的類別：
=IMROUND(IMPRODUCT(H2,IMSQRT(L2),IMSQRT(M2),IMSQRT(N2)),6)
當q√L√M√N<0時為A類方程，q√L√M√N>0時為B類方程，q√L√M√N=0時為AB類方程。
P欄為A類方程第一個根：
=IMROUND(IMSUM(-B2/(4*A2),IMSQRT(L2),IMSQRT(M2),IMSQRT(N2)),6)
Q欄為A類方程第二個根：
=IMROUND(IMSUM(-B2/(4*A2),IMSQRT(L2),IMOPPSITE(IMSQRT(M2)),IMOPPSITE(IMSQRT(N2))),6)
R欄為A類方程第三個根：
=IMROUND(IMSUM(-B2/(4*A2),IMOPPSITE(IMSQRT(L2)),IMSQRT(M2),IMOPPSITE(IMSQRT(N2))),6)
S欄為A類方程第四個根：
=IMROUND(IMSUM(-B2/(4*A2),IMOPPSITE(IMSQRT(L2)),IMOPPSITE(IMSQRT(M2)),IMSQRT(N2)),6)
T欄為B類方程第一個根：
=IMROUND(IMSUM(-B2/(4*A2),IMSQRT(L2),IMSQRT(M2),IMOPPSITE(IMSQRT(N2))),6)
U欄為B類方程第二個根：
=IMROUND(IMSUM(-B2/(4*A2),IMSQRT(L2),IMOPPSITE(IMSQRT(M2)),IMSQRT(N2)),6)
V欄為B類方程第三個根：
=IMROUND(IMSUM(-B2/(4*A2),IMOPPSITE(IMSQRT(L2)),IMSQRT(M2),IMSQRT(N2)),6)
W欄為B類方程第四個根：
=IMROUND(IMSUM(-B2/(4*A2),IMOPPSITE(IMSQRT(L2)),IMOPPSITE(IMSQRT(M2)),IMOPPSITE(IMSQRT(N2))),6)
當方程為AB類時，PQRS欄和TUVW欄都是方程的根。
X欄檢驗A類方程第一個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,P2,P2,P2,P2),IMPRODUCT(B2,P2,P2,P2),IMPRODUCT(C2,P2,P2),IMPRODUCT(D2,P2),E2),6)
Y欄檢驗A類方程第二個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,Q2,Q2,Q2,Q2),IMPRODUCT(B2,Q2,Q2,Q2),IMPRODUCT(C2,Q2,Q2),IMPRODUCT(D2,Q2),E2),6)
Z欄檢驗A類方程第三個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,R2,R2,R2,R2),IMPRODUCT(B2,R2,R2,R2),IMPRODUCT(C2,R2,R2),IMPRODUCT(D2,R2),E2),6)
AA欄檢驗A類方程第四個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,S2,S2,S2,S2),IMPRODUCT(B2,S2,S2,S2),IMPRODUCT(C2,S2,S2),IMPRODUCT(D2,S2),E2),6)
AB欄檢驗B類方程第一個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,T2,T2,T2,T2),IMPRODUCT(B2,T2,T2,T2),IMPRODUCT(C2,T2,T2),IMPRODUCT(D2,T2),E2),6)
AC欄檢驗B類方程第二個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,U2,U2,U2,U2),IMPRODUCT(B2,U2,U2,U2),IMPRODUCT(C2,U2,U2),IMPRODUCT(D2,U2),E2),6)
AD欄檢驗B類方程第三個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,V2,V2,V2,V2),IMPRODUCT(B2,V2,V2,V2),IMPRODUCT(C2,V2,V2),IMPRODUCT(D2,V2),E2),6)
AE欄檢驗B類方程第四個根的誤差：
=IMROUND(IMSUM(IMPRODUCT(A2,W2,W2,W2,W2),IMPRODUCT(B2,W2,W2,W2),IMPRODUCT(C2,W2,W2),IMPRODUCT(D2,W2),E2),6)

其中用到的三個自定義函數（按Alt+F11，在彈出的窗口中添加模塊）：
Function IMCBRT(x, Optional w As Integer = 0)
    If WorksheetFunction.Imaginary(x) = 0 Then
        IMCBRT = WorksheetFunction.Power(x, 1 / 3)
    Else
        IMCBRT = WorksheetFunction.ImPower(x, 1 / 3)
    End If
   
    If w Mod 3 = 1 Then
        w1 = WorksheetFunction.Complex(-1 / 2, VBA.Sqr(3) / 2)
        IMCBRT = WorksheetFunction.ImProduct(w1, IMCBRT)
    ElseIf w Mod 3 = 2 Then
        w2 = WorksheetFunction.Complex(-1 / 2, -VBA.Sqr(3) / 2)
        IMCBRT = WorksheetFunction.ImProduct(w2, IMCBRT)
    End If
End Function
Function IMROUND(x, Optional n As Integer = 0)
    real = WorksheetFunction.Round(WorksheetFunction.ImReal(x), n)
    imag = WorksheetFunction.Round(WorksheetFunction.Imaginary(x), n)
    IMROUND = WorksheetFunction.Complex(real, imag)
End Function
Function IMOPPSITE(x)
    If x = 0 Then
        IMOPPSITE = 0
    Else
        real = -WorksheetFunction.ImReal(x)
        imag = -WorksheetFunction.Imaginary(x)
        IMOPPSITE = WorksheetFunction.Complex(real, imag)
    End If
End Function
函數的用法：
IMCBRT(x)求x的算術立方根，IMCBRT(x,1)和IMCBRT(x,2)求x的其他兩個立方根
IMROUND(x,n)讓複數x四捨五入保留n位小數
IMOPPSITE(x)求複數x的相反數-x

AB類方程
一元四次方程分為三類：A類、B類、AB類。
AB類方程屬於簡單四次方程。A類、B類方程屬於複雜四次方程。
若一個一元四次方程滿足q√L√M√N=0，這個方程就是AB類方程。且q√L√M√N=0一定是因為q=0。（q的分子為8a²d-4abc+b³）
AB類方程之所以又叫簡單四次方程，是因為這類方程形式上非常簡單，主要包括
（1）只含四次項和常數項的方程：ax4+e=0
證明：因為b=c=d=0，q的分子為0，所以q=0，方程屬於AB類
（2）雙二次方程：ax4+cx2+e=0
證明：因為b=d=0，q的分子為0，所以q=0，方程屬於AB類
（3）能直接用配四次方法求解的四次方程，如x4+4x3+6x2+4x-5=0，可以配成(x+1)4-6=0
證明：方程能用配四次方法直接求解，說明x=y-b/4a換元後得到的方程y4+py2+qy+r=0不含三、二、一次項。因此p=q=0。因q=0，所以方程屬於AB類
配平方法和待定係數法得到的求根公式無法求解AB類四次方程。 [2]
證明：這個命題等價於「無論p和r為何值，若q=0，則分母2y-p=0，利用求根公式無法計算x的值」。
在前面的推導過程中已經知道配平方法和待定係數法得到的公式是等價的，所以下面僅考慮配平方法的公式。
推導過程中關於y的三次方程是8y³-4py²-8ry+4pr-q²=0，顯然當q=0時，y=p/2是方程的一個根。
但三次方程一共有三個根，y=p/2隻是其中一個根。需要證明根據y的公式算出來的y確實等於p/2，而不是三次方程的其他兩根，否則沒有說服力。
y的公式裡面含有兩個三次根號，每個三次根號裡面又含有一個二次根號。二次根號裡面的內容是相同的。
當q=0時，二次根號裡面的內容是(2p³-72pr)²-4(p²+12r)³，展開後是-432p4r+3456p2r2-6912r3。提取公因式-432r，得到-432r(p4-8p2r+16r2)，括號內是一個完全平方式，於是因式分解成-432r(p²-4r)²。
這下二次根號就可以開出來一些因式了。因為432=12×12×3，所以√[-432r(p²-4r)²]=12(p²-4r)√(-3r)。
第一個三次根號裡面就可以化簡成：p³-36pr+6(p²-4r)√(-3r)
第二個三次根號裡面可以化簡成：p³-36pr-6(p²-4r)√(-3r)
開三次方的結果分別為p+2√(-3r)和p-2√(-3r)。
所以y=[p+p+2√(-3r)+p-2√(-3r)]/6=3p/6=p/2 => 2y-p=0，得證。
這充分說明，配平方法和待定係數法得到的求根公式無法求解所有的一元四次方程。
只有x=u+v+w法得到的只含三層根號的求根公式，才能求解所有的一元四次方程。對於AB類簡單方程，q=0，且u、v、w這三個數中肯定有一個為0，所以±u±v±w只能算出四種結果，對應方程的四個根。
A類、B類複雜方程，q、u、v、w都不為0，±u±v±w算出來是八種結果，其中四種結果是方程的四個根，另外四種結果是增根。
對於實係數四次方程，計算出來的p、q、r也是實數，對應的三次方程也是實係數，三次方程的三根u²、v²、w²只有兩種情況：①三個都是實數；②一個實數，一對共軛虛數。所以uvw相乘一定是實數，不會出現uvw相乘為虛數，無法判斷方程類別的情況。
x=u+v+w法得到的四次方程求根公式中含有虛數i的原因：u²、v²、w²是某三次方程的三根，而三次方程求根公式裡面，第一個根的公式不含虛數i，而第二、第三個根的公式含有虛數i。

Excel表格建好後，隨意輸入一元四次方程的五個係數：a、b、c、d和e，可以發現此Excel表能正確判斷方程的類型（A類、B類或AB類），並且檢驗出來四個解中每個解的實部和虛部的誤差（也就是把算出來的x代回原方程的左邊，看計算結果與右邊的0相差有多大）都小於10^-5甚至10^-6。

這充分說明之前推導的「只含有三層根號的一元四次方程求根公式」雖然公式中含有虛數i，但是仍能正確求解出未知數的值（包括實數解）。

從圖中可以看出，A類方程的4個A類根的誤差幾乎為0，但是4個B類根（增根）的誤差非常大。
B類方程正好相反，4個A類根是增根，誤差極大，4個B類根才是方程的解，誤差幾乎為0。

AB類簡單方程，A類根和B類根誤差都幾乎為0，沒有增根。仔細一看就會發現，A類根和B類根的四個數值是相同的。