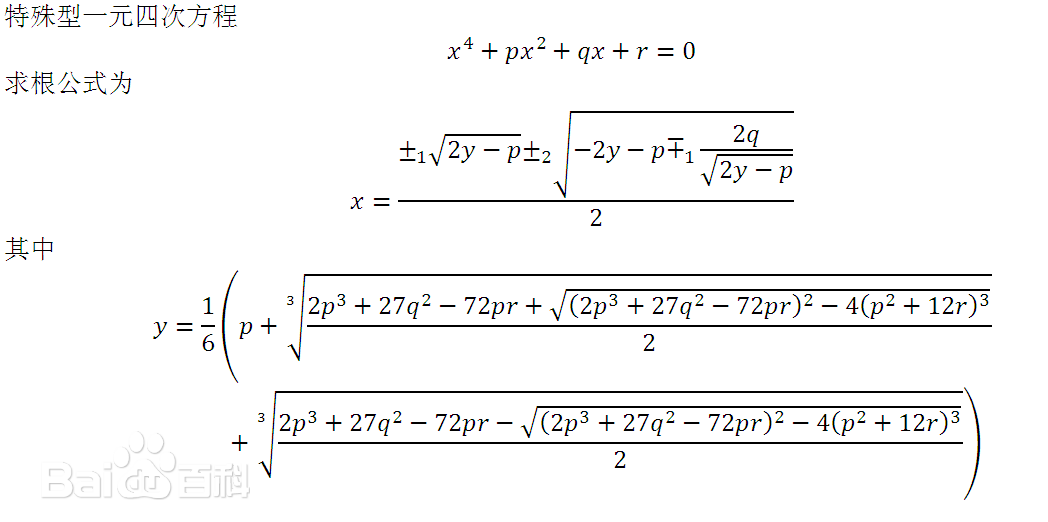對於特殊型一元四次方程x4+px2+qx+r=0，如果q=0，那麼這個方程就是AB類方程（簡單四次方程）。
AB類方程之所以又叫簡單四次方程，是因為這類方程形式上非常簡單，主要包括
（1）只含四次項和常數項的方程：ax4+e=0
因為b=c=d=0，q的分子為0，所以q=0，方程屬於AB類
（2）雙二次方程：ax4+cx2+e=0
因為b=d=0，q的分子為0，所以q=0，方程屬於AB類
（3）能直接用配方法求解的四次方程，如x4+4x3+6x2+4x-5=0，可以配成(x+1)4-6=0
方程能用配四次方法直接求解，說明x=y-b/4a換元後得到的方程y4+py2+qy+r=0不含三、二、一次項。因此p=q=0。因q=0，所以方程屬於AB類

配平方法和待定係數法得到的求根公式無法求解AB類四次方程。
證明：這個命題等價於「無論p和r為何值，若q=0，則分母2y-p=0，利用求根公式無法計算x的值」。
在前面的推導過程中已經知道配平方法和待定係數法得到的公式是等價的，所以下面僅考慮配平方法的公式。
推導過程中關於y的三次方程是8y³-4py²-8ry+4pr-q²=0，顯然當q=0時，y=p/2是方程的一個根。
但三次方程一共有三個根，y=p/2隻是其中一個根。需要證明根據y的公式算出來的y確實等於p/2，而不是三次方程的其他兩根，否則沒有說服力。

如上圖所示，y的公式裏面含有兩個三次根號，每個三次根號裏面又含有一個二次根號。二次根號裏面的內容是相同的。
當q=0時，二次根號裏面的內容是(2p³-72pr)²-4(p²+12r)³，展開後是-432(p^4)r+3456p²r²-6912r³。提取公因式-432r，得到-432r(p^4-8p²r+16r²)，括號內是一個完全平方式，於是因式分解成-432r(p²-4r)²。
這下二次根號就可以開出來一些因式了。因為432=12×12×3，所以√[-432r(p²-4r)²]=12(p²-4r)√(-3r)。
第一個三次根號裏面就可以化簡成：p³-36pr+6(p²-4r)√(-3r)
第二個三次根號裏面可以化簡成：p³-36pr-6(p²-4r)√(-3r)
開三次方的結果分別為p+2√(-3r)和p-2√(-3r)。
所以y=[p+p+2√(-3r)+p-2√(-3r)]/6=3p/6=p/2 => 2y-p=0，得證。
這充分說明，配平方法和待定係數法得到的求根公式無法求解所有的一元四次方程。