计算机如何自动计算不定积分,是一个长期感兴趣的问题,1968年出现的Risch算法,以及在1976年的改进Risch–Norman算法在相当程度上解决了这个问题,这些算法可以自动求解初等函数的不定积分,前提是积分也是初等函数。
目前共有20篇帖子。
目前共有20篇帖子。
 |
参考:https://www-sop.inria.fr/cafe/Manuel.Bronstein/publications/issac98.pdf
|
 |
第一种情况,有理函数的积分。
有理函数是两个多项式的商。根据代数基本定理,多项式一定能在代数闭域内分解为一次多项式的乘积,而在实数域内,则分解成一次多项式和判别式为负数的二次多项式的乘积:  |
 |
如果上述D是有理函数的分母,那么通过所谓部分分式展开,可以把有理函数写成下列形式
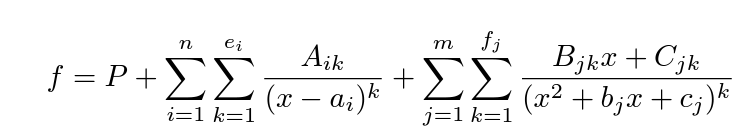 其中P是多项式,Aik,Bjk,Cjk,ai,bj,cj都是实数。 那么,要计算这个积分,只需要分别计算每一项的积分即可。多项式P的积分容易计算;其余各项的积分如下: 1. 分母为一次式的k次方:  2. 分母为二次式,k=1: 2. 分母为二次式,k=1: 这里的判别式4cj-bj^2<0. |
 |
3. 分母为二次式,k>1:
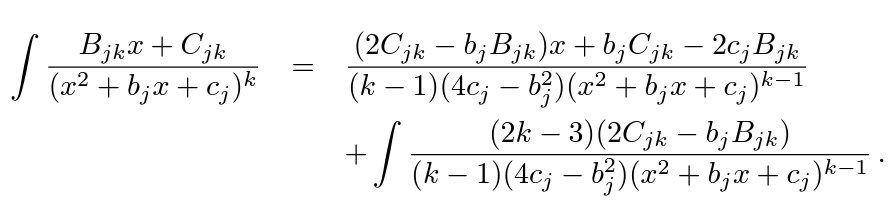 这样就可以递推式地降低k,直到k=1. |
 |
这种算法有一个重大缺陷:并没有什么算法可以得到所需的因式分解。这并不是说因式分解不存在,而是我们无法通过一种算法求解它。例如,五次方程x^5-x+1=0就没有根式解。(即使通过特殊函数,也会涉及希尔伯特第十三问题而难以解决)
为了解决这个问题,我们首先需要对分母的因式分解进行限制,保证其有相应的算法。 巨大八爪鱼:从三次方程开始,精确的根式解就很复杂了,有的解含有虚数i,有的解要用双层根号表示。甚至要用含有根号和虚数i的式子来表示一个实数。
巨大八爪鱼:另外,高次方程经常会遇到实部和虚部都是无理数的虚数解,有时这些无理数要用多层根号表示(三、四次方程)(根号里面还可能含有虚数i),有时甚至完全无法用根号表示(五次方程以上),只能用有限小数近似值加省略号表示。
[查看詳情]
|
 |
如果多项式f有不可约因式g^m, 但g^{m+1}不是f的因式,那么f和f导数f'的公因式(f,f')能被g^{m-1}整除,但不能被g^m整除。 我们用这个事实,可以得知公因式h=(f,f')的每个不可约因式的次数比f小1. |
 |
我们假设f是首一多项式,把相同重数的不可约因式放在一起,设
那么,首一公因式(f,f')为
于是,我们有
|
 |
 上述算法成功把分母的最高重数从m降到了m-1,因此重复上述步骤,就可以把有理积分化约为分母无平方因子的情况。这叫做厄尔米特约化(Hermite reduction)。 |
 |
根据厄尔米特约化,我们只需要求A/D, deg(A)<deg(D), D无平方因子,这种情况的不定积分。
我们考虑在复数域内对D进行分解,结果是互不相同(因为D无平方因子)的单项式的乘积,因此A/D有部分分式展开
此时,使用复对数,可以把积分表示为 其中C是任意常数。当然,我们是不会满足于这种表示的,因为它很明显仍然没有规避高次方程求根的问题。 |
 |
这里的ai显然等于A/D在单极点ri的留数。设D=D1(x-ri), 那么不难计算出
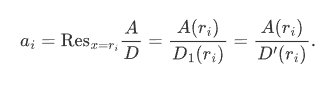 因此,ri是D和A-aiD'的公共零点。根据结式(https://zh.wikipedia.org/wiki/%E7%B5%90%E5%BC%8F)的性质,ai恰好就是结式 的根(即使得上述结式等于零的t)。 |