但是上述算法仍然可以改進。實際上,我們不需要直接對R進行不可約分解,先進行無平方因子分解也是可以的:

我們有

其中pp是指多項式的「本原部分」,也就是多項式乘以一個適當的數以後,得到的以互素整元素為係數的新多項式。Rki是所謂「子結式」。兩個多項式的子結式是以它們的結式開始的,一系列以它們的係數為變量的,次數遞減的多元多項式,其滿足的性質是:兩個多項式有k個公共零點,若且唯若其前k個子結式為零。
這個結果還是不可避免地出現了一些無法求出的高次方程的根,但我們已經可以基本上僅僅用它們表示結果而不是對它們進行實際計算。即使是對本原部分(pp)的計算,也是可以避免的,參考T. Mulders. A note on subresultants and a correction to the LazardRioboo–Trager formula in rational function integration. Journal of Symbolic Computation, 24(1):45–50, 1997.

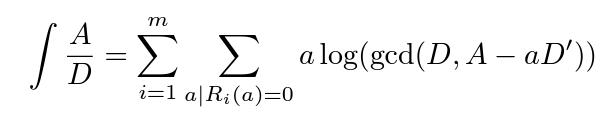 很明顯,這個結果並非完美。我們仍然需要使用Ri的根來表示這個結果,而不可約多項式Ri仍然可能是高次的不可求根式解的多項式。但已經證明,要把這個不定積分表示成初等函數,我們至少需要在R在K上的分裂域上表示。因此,這個結果理論上已經是最簡化的。
很明顯,這個結果並非完美。我們仍然需要使用Ri的根來表示這個結果,而不可約多項式Ri仍然可能是高次的不可求根式解的多項式。但已經證明,要把這個不定積分表示成初等函數,我們至少需要在R在K上的分裂域上表示。因此,這個結果理論上已經是最簡化的。