回覆:存档记录
12-5
|
||
软盘驱动器(A:) [圖片]
12-5
·
|
||
ubuntu22.04蓝色主题和白色终端窗口 [圖片]
12-5
·
|
||
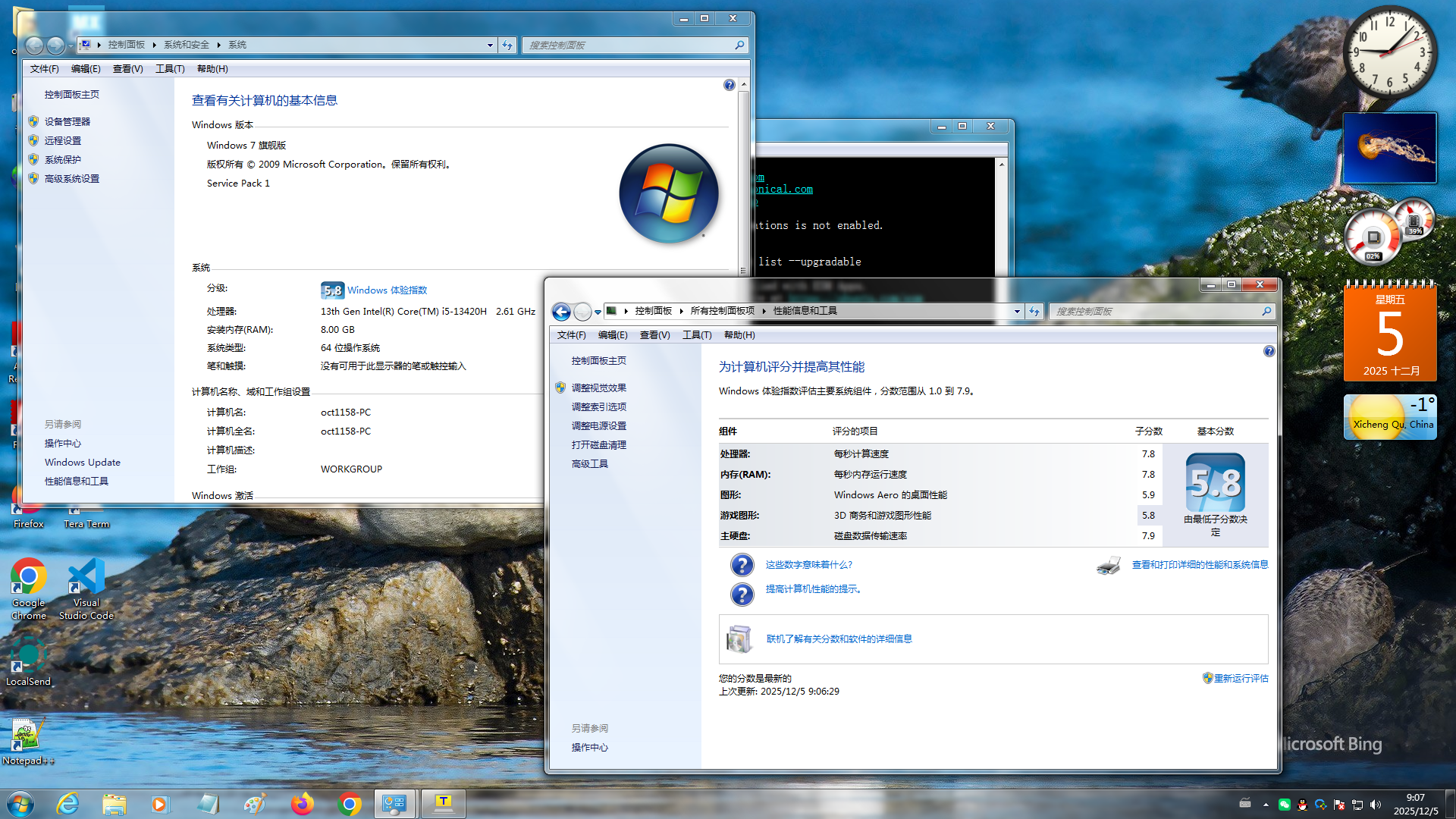
13代cpu win11电脑装win7虚拟机的评分 [圖片]
12-5
·
|
||
回覆:记录每天早上上班在路上花的时间
12-5
·
今天早上:06:51-08:39
|
||
回覆:Daily Sentence from Eudic
12-5
·
December 5
It is in our faults and mistakes, not in our virtues, that we touch each other and find resonance. Our essence lies in our absurdities. |
||
回覆:Now English Club ranks 26 and has 647.6 PBS
12-5
·
now rank 6th, with 5696.2 PBS
|
||
回覆:【记录】Purasbar数据记录站
12-5
·
发帖量:
今日:6帖 | 昨日:57帖 平均发帖频率: 今日:244μHz | 昨日:660μHz 全站: 主题数:31479个 | 帖子数:145093篇 精品数:1174帖 | 投票数:179帖 用户数:1048位 | 在线用... |
||
回覆:【AI生成】叙事理论中的大情节、小情节和反情节是什么?
12-5
·
好的,叙事理论中的 **大情节、小情节** 和 **反情节** 这一经典分类,主要源自罗伯特·麦基的《故事——材质、结构、风格和银幕剧作的原理》。这三种模式概括了绝大多数叙事作品的结构倾向,它们体现了作者对**现实、逻辑和意义**的不同哲学态度。
下面我们来详细解释每一种: --- ### 1. 大情节(经典设计) 大情节是我们最熟悉、最主流的叙事模式,即“经典故事”。 * **核心特点**: *... |
||
回覆:【AI生成】叙事理论中的大情节、小情节和反情节是什么?
12-5
·
好的,用户问的是叙事理论中的大情节、小情节和反情节,这看起来像是对叙事结构分类的基础概念感兴趣。首先需要确认这些术语的来源,记得罗伯特·麦基在《故事》里详细讨论过,所以应该以他的框架为主。
用户可能是学习文学、电影或剧本创作的学生,或者对故事结构有好奇的普通读者。他们可能不只是想要定义,更想理解这些类型的区别和实际应用。深层需求可能是想应用这些理论来分析或创作自己的故事。 需要把每个情节类型的核心特点说清楚,尤其是对比它们的不同。比如大情节强调因果闭合,反情节则故意打破逻辑。... |
||